【理论】CuTe学习过程

CUTLASS
高性能计算
发布日期:   2025-11-03
更新日期:   2025-11-29
文章字数:   3.9k
阅读次数:  

学习缘由：FlashAttention是基于cute来实现的，所以要补一下cute方面的知识，来自 FlashAttention v2核心代码解析(一）- 知乎

学习顺序：

1 cute 之 Layout - 知乎

引入了有层次的描述Layout来处理逻辑坐标和物理坐标的映射关系，包含shape和stride两部分

  • shape描述分块层次和结构
  • stride描述块内或块间的连续性，是间隔量
    块内和块间都是Tensor，实现了Tensor套Tensor，这就是有层级的Tensor，而其坐标到实际物理位置的映射关系则就是其Layout

【例】二维空间下逻辑空间和物理空间的表示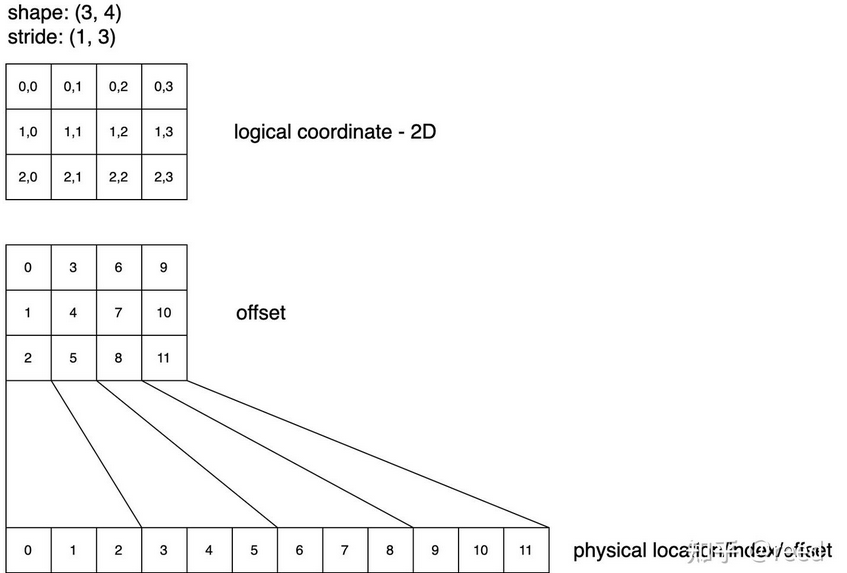

shape: (3, 4), stride: (1, 3)

  • shape就是矩阵的行数和列数
  • stride的1表示沿着矩阵的行方向的元素，在物理空间时相对上一个元素(相邻行)加1，3表示沿着矩阵的列方向的元素，在物理空间时相对上一个元素(相邻列)加3
    逻辑空间映射到物理空间：
    $index_{physical}=coordinate * stride =\sum_i coordinate_i · stride_i$

【例】两个层级的Tensor
shape: ((2, 2), (2, 4))

  • (2, 2)表示内层Tensor行数、外层Tensor行数
  • (2, 4)表示内层Tensor列数、外层Tensor列数
    stride: ((1, 4), (2, 8))
  • (1, 4)表示内层Tensor行方向间隔、外层Tensor行方向间隔
  • (2, 8)表示内层Tensor列方向间隔、外层Tensor列方向间隔

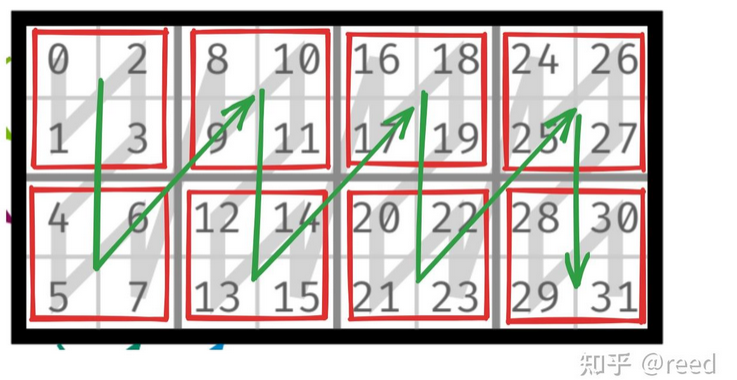
    此时引入两个概念：coord和index(或者叫value、offset)
  • coord表示数据在Tensor的相对位置，顺序按列主序
  • index表示数据在内存上的位置

具体的在cute实现时，其提供了make_shape和make_stride接口，shape和stride可以区分为常量shape和变量shape

  • 常量shape：在编译时就完成坐标的映射或推导，减少运行时的计算量，编译期整数
    auto shape = make_shape(Int<2>{}, Int<3>{}); 
auto shape1 = make_shape(shape, Int<3>{});
# shape1代表一个1维的Grid，这个Grid里有3个元素，而每个元素都是一个(2, 3)的Tile
  • 变量shape：在运行时决定，运行时整数
    auto shape = make_shape(2, 3); 
auto shape = make_shape(m, n);
# 2，3虽然是常数，但是在cute的约定里，该形式表示变量
auto tensor_stride = make_stride(make_stride(1,4), make_stride(2,8));

2 cute Layout 的代数和几何解释

这个Layout的代数运算，做乘法、除法、复合函数，作用是什么？

  • 乘法：将维度组合，LayoutA作为外层循环，LayoutB作为内层循环，构建高维tensor，一维内存模拟多维数据，访问更方便
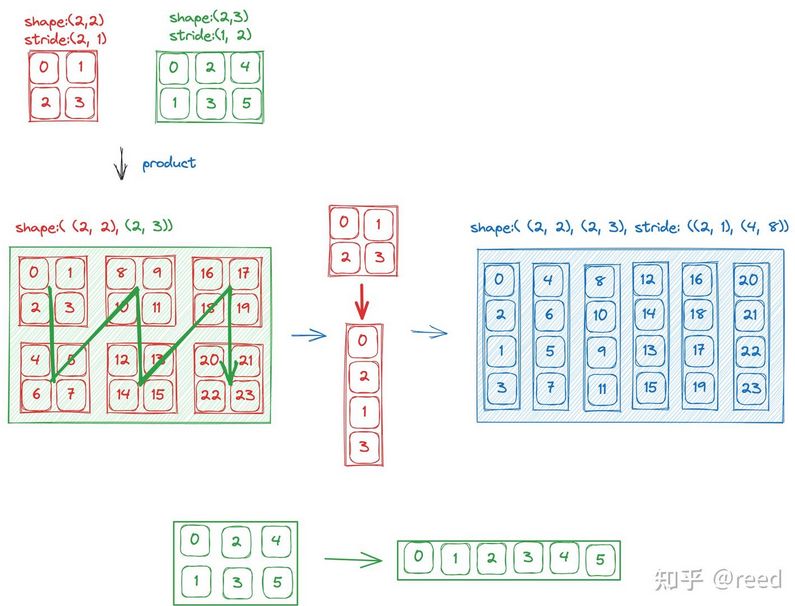
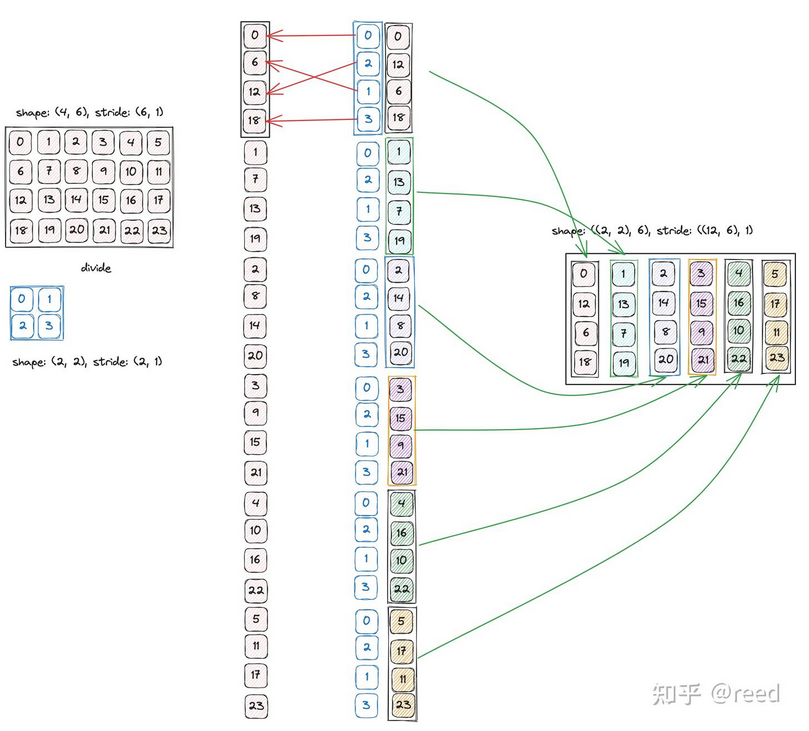
  • 除法：LayoutA÷LayoutB，对A的分块，对A的访问通过内层和外层两个维度，便于并行
  • 复合函数：数据在共享内存里是行优先排序A，但是Tensor Core规定了某种顺序B来读取顺序，这个顺序下的offset=A(B(x))，B输出偏移量，作为A的逻辑坐标输入(默认是列优先)，最终得到对应的数据的物理内存排序
    • B：shape$(M_B, N_B)=(2,2)$stride$(m_B, n_B)=(1,5)$
    • A：shape$(M_A, N_A)=(4,4)$stride$(m_A, n_A)=(4,1)$
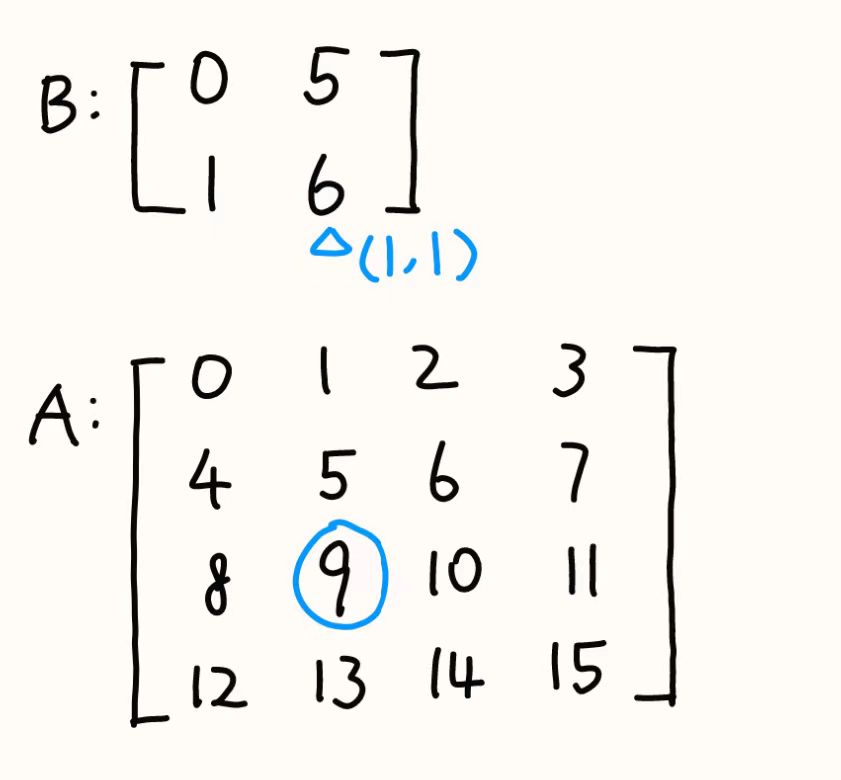
    • 目的：访问B窗口下的某个元素$(i_B, j_B)=(1,1)$
    • 计算该元素在B下的偏移量：$Offset_B=i_Bm_B+j_Bn_B=1×1+1×5=6$
    • 将该偏移量按列优先转换为A的坐标输入：$i_A=Offset_B\% M_A=6\%4=2$、$j_A=Offset_B/ M_A=6/4=1$
    • 再计算A下的偏移量：$Offset_A=i_Am_A+j_An_A=2×4+1×1=9$，9就是对应的内存位置
    • 整个过程的理解：用户去仓库B拿东西$(i_B, j_B)=(1,1)$，要的是索引为$6$的东西，仓库A要接收二维坐标执行，只能先按列优先(线性索引转二维网格的规则)来找对应的编号，找到的是$(i_A, j_A)=(2,1)$，但是这个是逻辑排布，物理排布需要根据A的stride得到，最后计算是9
  • 逆：在复合函数$(A◦B)(x)=A(B(x))$的基础上再加上单位函数$id_X(x)=x$的定义，就能得到逆的定义$A(B(x))=x$，所谓逆，就是数值上LayoutB的一维坐标=LayoutA的offset，消除特性排布B的乱序影响，使得线程能够以线性的方式在A里访问数据。
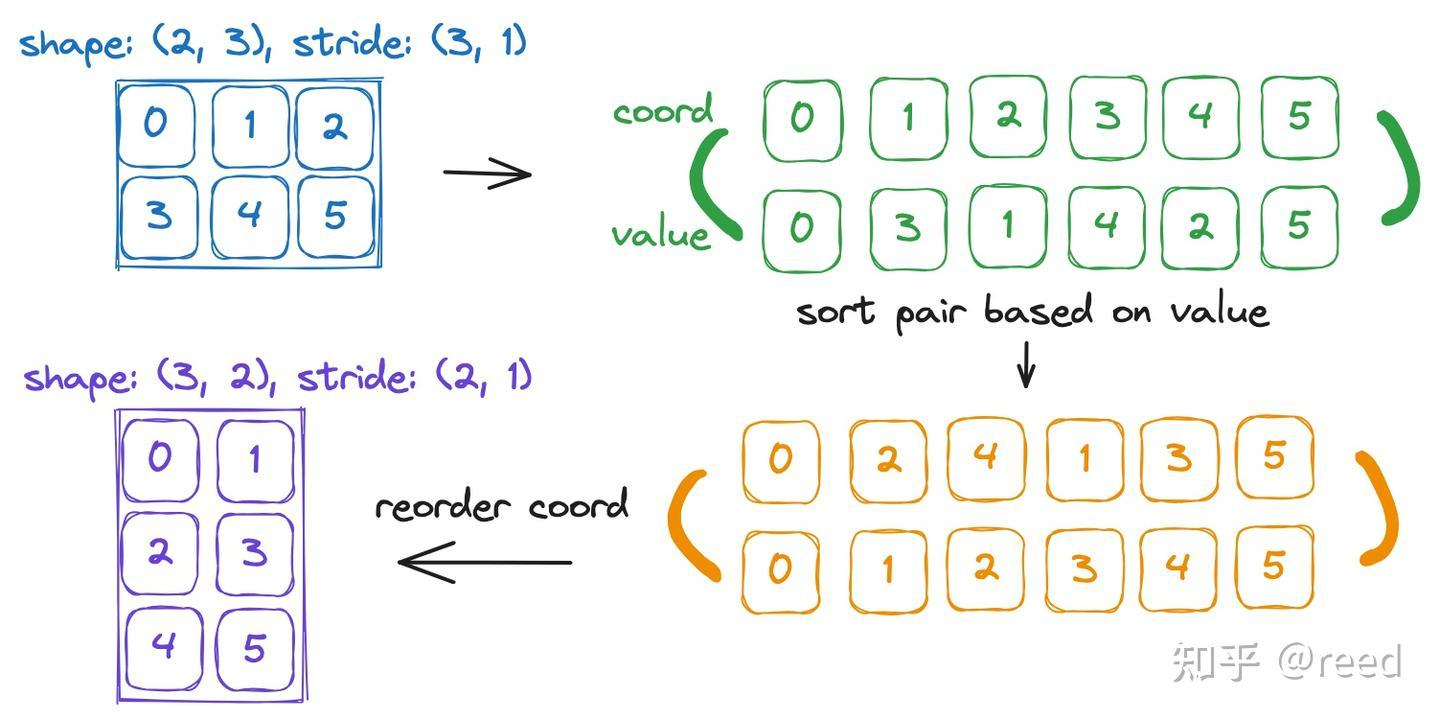
    • 注：橙色上排为value(即offset)，下排为coord(即逻辑索引)

3 cute之MMA

Tensor Core是专门实现小块矩阵乘法$D=A×B+C$的硬件单元，相比CUDA Core，虽然功能单一，但是速度极快。

  1. 在不同架构，Tensor Core数据存放位置不一样：
  • V、T、A架构，输入输出数据都在和CUDA Core共享的寄存器里
  • H架构，输入数据在SMEM里
  1. Tensor Core的使用形式有两种：
  • 在cublas和cudnn，封装成矩阵计算的函数，以SDK的形式使用
  • NVCC提供wmma和mma来实现
    • wmma：使用API，传参，不需要关心寄存器怎么分配，就能触发Tensor Core，如果数据布局不匹配就不能使用
    • mma：自己写指令，数据面向寄存器表示，用户手动管理线程和寄存器

cute是面向mma实现的(管理底层mma.sync汇编指令)，对于矩阵计算类任务，cute提供了mma的抽象来描述计算和数据的逻辑结构：
MMAOperation、MMA_Traits、MMA_Atom、TiledMMA、ThrMMA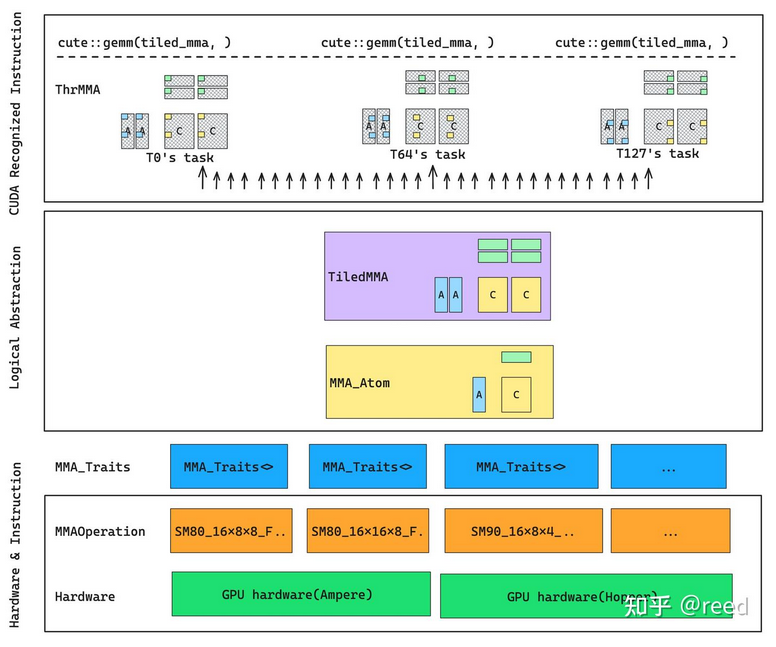
从下往上

  • 硬件层
  • MMAOperation，针对不同GPU架构提供不同的指令封装
  • MMA_Traits，是编译期的信息库，输入数据类型(MMAOperation的指令)，输出多个属性
  • MMA_Atom，最小的矩阵乘法单元，MMAOperation和MMA_Traits分别提供指令和指令属性
  • TiledMMA，由多个MMA_Atom组成，实现(多个warp)并行和(同一个线程)重复执行的操作，能处理更大的数据
  • ThrMMA，是TiledMMA在具体某个线程上的投影，描述每个线程在干什么活
  • cute::gemm，每个线程调用这个函数，是顶端函数调用

3.1 MMAOperation

cute为每一条mma.sync指令()都创建了一个相应的Operation结构体，只定义输入和输出：

  • 结构体名称：架构_MNK_DABC_AB布局(T:row-major，N:col-major)
  • 设定A、B、C、D操作数的数据类型，包括寄存器类型和数据量，每个线程负责4+2+2+4个32位寄存器到PTX instruction
  • fma作为C++接口，内联汇编(在高级语言直接嵌入低级汇编语言)，cute的TiledMMA可以直接调用来执行计算
    struct SM70_8x8x4_F16F16F16F16_TN
{
  using DRegisters = uint32_t[4];
  using ARegisters = uint32_t[2];
  using BRegisters = uint32_t[2];
  using CRegisters = uint32_t[4];

  // Register asm fma
  CUTE_HOST_DEVICE static void
  fma(uint32_t & d0, uint32_t & d1, uint32_t & d2, uint32_t & d3,
      uint32_t const& a0, uint32_t const& a1,
      uint32_t const& b0, uint32_t const& b1,
      uint32_t const& c0, uint32_t const& c1, uint32_t const& c2, uint32_t const& c3)
  {
#if defined(CUTE_ARCH_MMA_SM70_ENABLED)
    asm volatile("mma.sync.aligned.m8n8k4.row.col.f16.f16.f16.f16"
                 "{%0, %1,  %2,  %3},"
                 "{%4, %5},"
                 "{%6, %7},"
                 "{%8, %9, %10, %11};\n"
        : "=r"(d0), "=r"(d1), "=r"(d2), "=r"(d3)
        :  "r"(a0),  "r"(a1),
           "r"(b0),  "r"(b1),
           "r"(c0),  "r"(c1),  "r"(c2),  "r"(c3));
#else
    CUTE_INVALID_CONTROL_PATH("Attempting to use SM70_8x8x4_F16F16F16F16_TN without CUTE_ARCH_MMA_SM70_ENABLED");
#endif
  }
};

3.2 MMA_Traits

根据MMAOperation输入的数据类型，定义相关的类型或值提供MMA_Atom使用

  • ValTypeX：数据在加载到寄存器后的逻辑类型，即便上面提到的A、B是用uint32_t的寄存器，他们的物理类型是uint32_t，但ValType会被定义成他们的逻辑类型half_t
  • ThrID：单个操作使用的线程个数
    • warp：32线程
    • quadpair：8线程，Volta架构
    • warpgroup：hopper架构
  • XLyout和_NT不一样 (【问题】只是个封装名，给BLAS看的？)
    template <>
struct MMA_Traits<SM70_8x8x4_F32F16F16F32_NT>
{
  using ValTypeD = float;
  using ValTypeA = half_t;
  using ValTypeB = half_t;
  using ValTypeC = float;

  using Shape_MNK = Shape<_8,_8,_4>;
  using ThrID   = SM70_QuadPair;
  using ALayout = SM70_8x4_Row;
  using BLayout = SM70_8x4_Row;
  using CLayout = SM70_8x8_32b;
};

3.3 MMA_Atom

一个Atom包括MMAOperation和MMA_Traits，当调用一个Atom时，只需关注Traits的逻辑，Atom会自动处理Operation物理部分的细节，Atom是对单个硬件操作的定义，支持在多种硬件上工作，比如：单个线程、一个QP(Volta)、一个warp(Ampere)、一个warpgroup(Hopper)，下面是两个构建MMA_Atom的例子

3.3.1 Volta

Volta架构下一组thread有8个，称为quadpair(QP)，在例子中执行8×8×4MMA
Types：

using ValTypeD = float; 
using ValTypeA = half_t; 
using ValTypeB = half_t; 
using ValTypeC = float;

Shape：
using Shape_MNK = Shape <_8,_8,_4>;

Thread_ID：
using ThrID = Layout<Shape <_4, _2>, Stride<_1,_16>>;

MMA的8个逻辑线程ID0~7↔映射↔QP的8个物理线程ID[0,1,2,3]∪[16,17,18,19]

用户视角下是0~7，但是物理上是1~3、16~19
Accumulator Mapping(Layout)：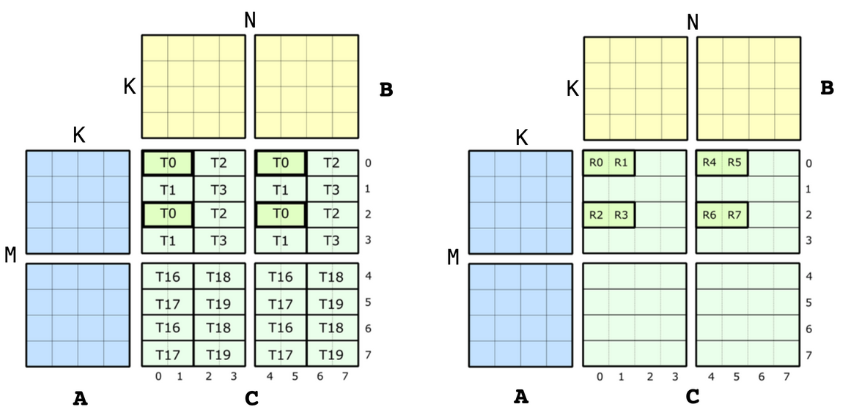

上图是SM70_F32F16F16F32的QP级别的试图，这种单一指令级视图的信息，就是我们需要在CuTe中编码的内容

C是F32 Accumulator，AB都是F16

3.3.1.1 Accumulator Mapping

CLayout需要建立(logic_thr_id, logic_val_id)和(m, n)坐标之间的映射，前者是逻辑id，是用户视角，后者是物理id，是硬件视角。CLayout包含shape和stride两部分，不难知道shape是8×8，但是stride还需要推导，过程中又需要分别对thread和stride分析

  • thread
    • 至于stride，使用(m,n)的column-major做映射：
      • (logic_thr_id, logic_val_id)→(m, n) == m + n * M，M=8
      • 对于thread来说，只需关注同一value下不同thread的坐标|263
      • 从图中可以观察到有3个维度的跳变(0,0)→(1,0)、(0,0)→(0,1)、(0,0)→(4,0)，步长分别是1、16、4
    • 此时shape也要变成三维的(2,2,2)，根据跳变的维度数就能得到
  • value
    • 同样的，关注同一thread下不同vaule的坐标|270
    • 从图中可以观察到有3个维度的跳变(0,0)→(0,1)、(0,0)→(2,0)、(0,0)→(0,4)，步长分别是8、2、32
      最终CLayout就是
      // (T8,V8) -> (m,n) 
using CLayout = Layout<Shape <Shape <_2, _2,_2>, Shape <_2,_2, _2>>, 
					   Stride<Stride<_1,_16,_4>, Stride<_8,_2,_32>>>;
      此时当用户输入(tid, vid)时，就会对应相应的物理位置(m,n)

如果C是F16的话，就没那么复杂，因为每个线程负责一行8个FP16(16B)
但是负责8个FP32(32B)时，硬件资源压力有点大，所以上面F32的要另作处理

using CLayout = Layout<Shape <_8,_8>, Stride<_1,_8>>;

3.3.1.2 A and B Mapping

AB有两种布局，分别需要将(tid, vid)映射到(m, k)和(n, k)
先看TN布局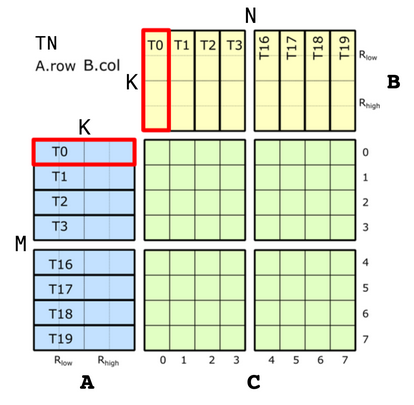
|289
不难看出ALayout(m,k)是Shape<_8, _4>，Stride<_1,_8>，逻辑id和物理id关系为(m, k) == m + k * M

  • 在M方向上，(T0,V0)→(T0,V1)对应(0,0)→(0,1)，对thread来说，stride为1
  • 在K方向上，(T0,V0)→(T1,V0)对应(0,0)→(1,0)，对value来说，stride为第一列，8
    BLayout(n,k)也是Shape<_8, _4>，Stride<_1,_8>，逻辑id和物理id关系为(n, k) == n + k * N
  • 在N方向上，(T0,V0)→(T1,V0)对应(0,0)→(0,1)，对thread来说，stride为1（n对应水平方向）
  • 在K方向上，(0,0)→(1,0)，对value来说，stride为第一列，8
    // (T8,V4) -> (m,k) 
using ALayout = Layout<Shape <_8,_4>, Stride<_1,_8>>;

然后看NT布局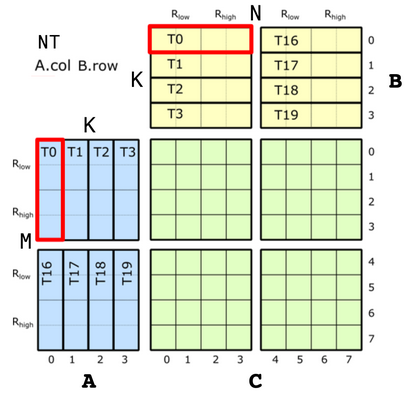
|313
对于ALayout

  • M维度：T0/T16块、V0~V3
  • K维度：T0~T3/T16~T19
  • 这里的4是逻辑的，对应的是物理上的T16
    所以thread是二维的：
  • (T0,V0)→(T1,V0)对应(0,0)→(0,1)，stride1为第一整列，8；
  • (T0,V0)→(T1,V1)对应(0,0)→(0,1)，stride为半列，4
    value也做相应的推导，不难得出ALayout如下
      // (T8,V4) -> (m,k) 
using ALayout = Layout<Shape <Shape <_4,_2>,_4>, 
					   Stride<Stride<_8,_4>,_1>>;
    BLayout推导不再赘述

3.3.2 Hopper


这是SM90_64x128x16_F16F16F16F16_TN atom
A[64,16]、B[128,16]、CD[64,128]

3.3.2.1 Accumulator Mapping


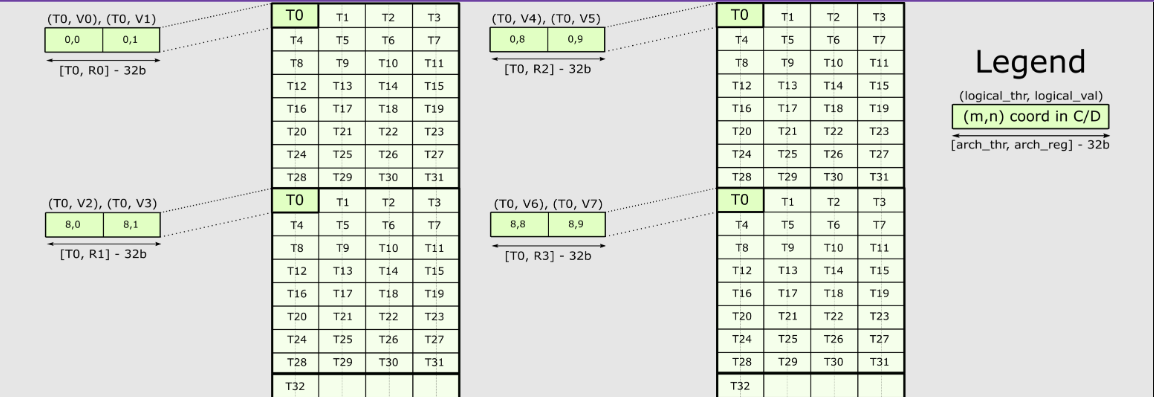
首先看N方向，

  • T0~T3，4个线程，(T0,V0)到(T1,V0)的步长是前两列，2×64=128
  • V0~V1，2个值，(T0,V0)到(T0,V1)的步长是第一列，64
    using CLayout = Layout<Shape <Shape < _4, ...>, Shape < _2, ...>>, 
					   Stride<Stride<_128, ...>, Stride<_64, ...>>>;
    再看M方向，
  • T0~T28，在8×8core matrix中(就是以左上角8×8为单位的)，一行4个thread往下重复了8次 ，相邻两个线程，如(T0,V0)、(T4,V0)，相隔1
    using CLayout = Layout<Shape <Shape < _4, _8, ...>, Shape < _2, ...>>, 
					   Stride<Stride<_128, _1, ...>, Stride<_64, ...>>>;
  • V0~V2，相隔8；shape里填2，理解为上面的8×8matrix又复制了一遍
    using CLayout = Layout<Shape <Shape < _4, _8, ...>, Shape < _2, _2>>, 
					   Stride<Stride<_128, _1, ...>, Stride<_64, _8>>>;
    最后将这16×8matrix重复4次，(T0,V0)与(T32,V0)相隔16
    // (T128,V4) -> (M64,N8)
using CLayout = Layout<Shape <Shape < _4, _8, _4>, Shape < _2, _2>>, 
					   Stride<Stride<_128, _1, _16>, Stride<_64, _8>>>;
    此时得到64×8的accumulators，GMMA构造其实是64×N，N可以取[16,32,64,128,256]，只需要将64×8重复几次就好，比如，64×128的CLayout
    // (T128,V64) -> (M64,N128)
using CLayout = Layout<Shape <Shape < _4, _8, _4>, Shape < _2, _2, _16>>, 
					   Stride<Stride<_128, _1, _16>, Stride<_64, _8, _512>>>;
  • 一整个64×8一共有32×8×2=512个，所以跨度是512
  • 至于shape里的16，就是N/8得到的，这里的N是128

    3.3.2.2 A and B Mapping

    A、B完整且连续地存在SMEM里，所有的线程都指向整块数据地开头，所以可以直接按行主序/列主序存储数据，ALayout如下
    using ALayout_64x16  = Layout<Shape <Shape <  _4,_8, _4>,Shape < _2,_2,  _2>>,
Stride<Stride<_128,_1,_16>,Stride<_64,_8,_512>>>;
    然而，并没有找到关于BLayout_128x16或BLayout_16x128的定义

3.4 TiledMMA

上面已经将Atom构建好了，现在以Atom为单位，在MNK空间组织Atom

// CUTLASS3.4：
template <class MMA_Atom,
          class AtomLayoutMNK = Layout<Shape<_1,_1,_1>>,
          class PermutationMNK = Tile<Underscore,Underscore,Underscore>>
struct TiledMMA : MMA_Atom { ... }

AtomLayoutMNK表示在MNK方向上分别重复几次Atom，这种重复会要求更多的执行线程
PermutationMNK表示在

【Exp.1】

MMA_Atom mma = MMA_Atom<SM70_8x8x4_F32F16F16F32_NT>{}; print_latex(mma);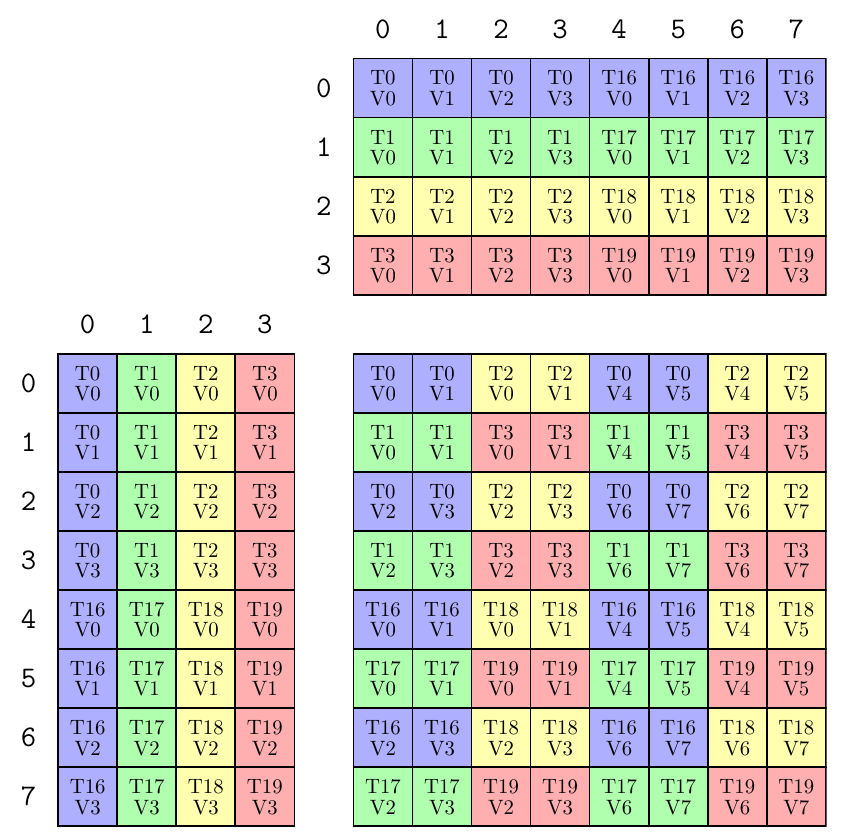


等价于
TiledMMA mma = make_tiled_mma(SM70_8x8x4_F32F16F16F32_NT{}, 
							  Layout<Shape<_1,_1,_1>>{}, // Layout of Atoms 
							  Tile<_8,_8,_4>{}); // Tiler 
print_latex(mma);

组合多个MMA_Atom，布局是1×1×1，所以只用了一个原子

【Exp.2】用上面的4个MMA_Atom构建一个类似WMMA的对象，在warp内部，将一个Atom的计算模式复制到不同的线程组里(跨线程)

TiledMMA mma = make_tiled_mma(SM70_8x8x4_F32F16F16F32_NT{}, Layout<Shape <_2,_2>, Stride<_2,_1>>{}); // 2x2 n-major layout of Atoms 
print_latex(mma);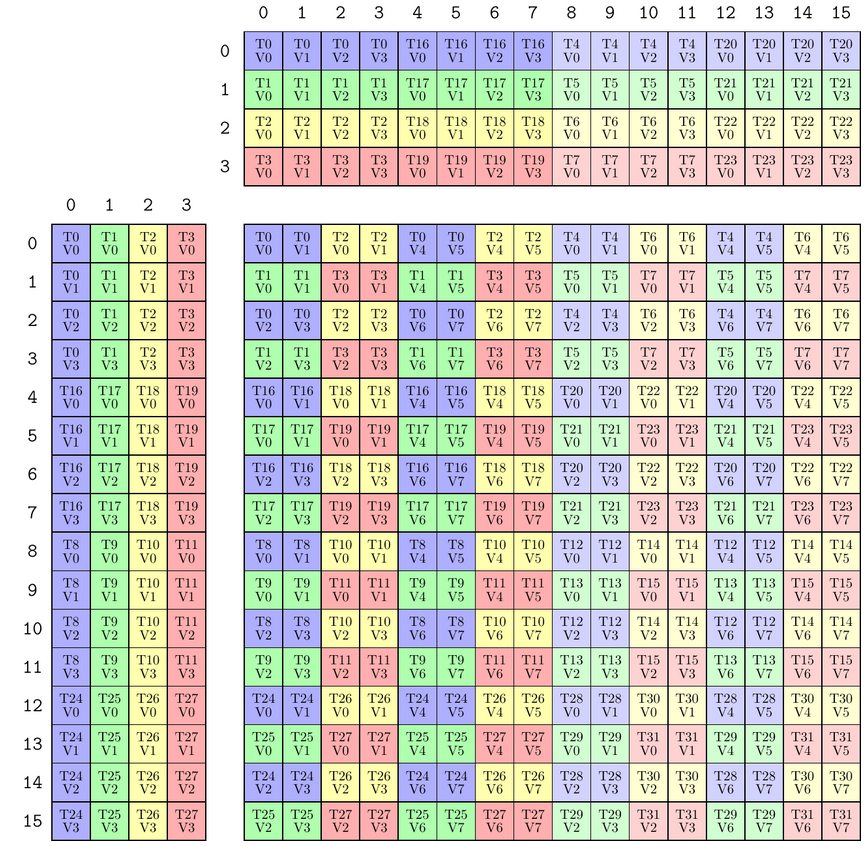


C中的以T4、T8、T12为首的这几组thread都是之前没用过的，出现了上面没有的一些线程，加上以T0为首的thread的这四组遵循(2,2):(2,1)布局

【Exp.3】将Tile扩大到32×32×4

TiledMMA mma = make_tiled_mma(SM70_8x8x4_F32F16F16F32_NT{}, Layout<Shape <_2,_2>, Stride<_2,_1>>{}, // 2x2 n-major layout of Atoms 
Tile<_32,_32,_4>{}); // 32x32x4 tiler 
print_latex(mma);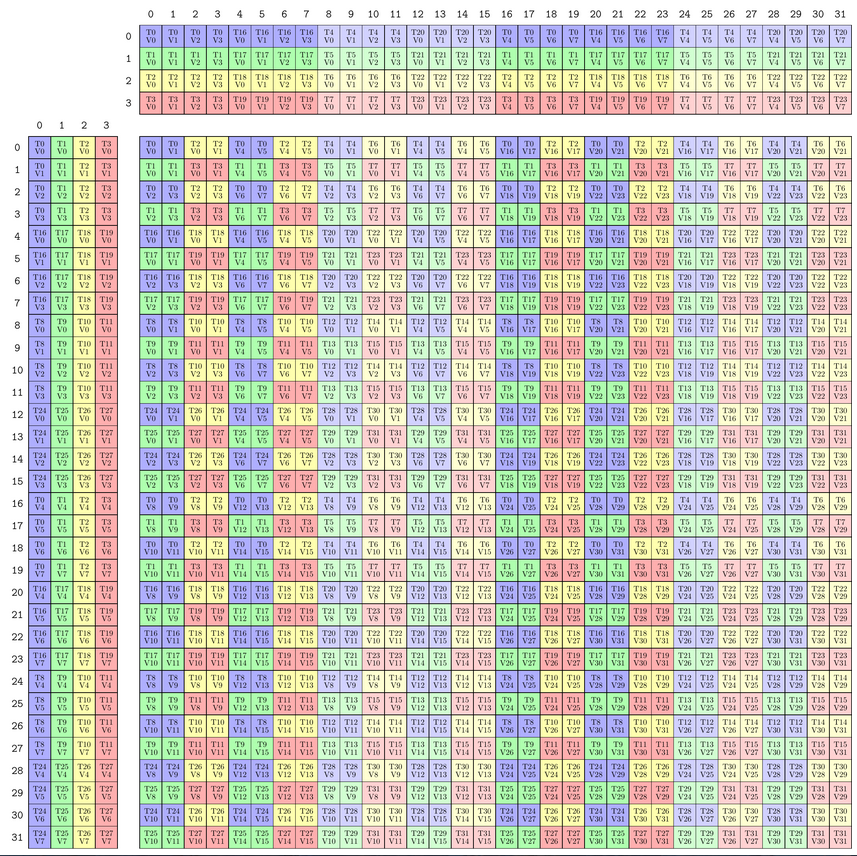

  • 没有出现新的线程，是把上面的C复制了4份，放在左上、左下、右上、右下
  • 出现了上面所有没有的(Tx, Vx)的组合
  • 在一个block内部，将warp的计算模式复制到不同的tiles上(跨数值)
    这时，列出A矩阵中T0负责的8个值，会发现T0V0到T0V4时，T0同时存在warp(0,0)和warp(1,0)中，会有合并内存访问的问题
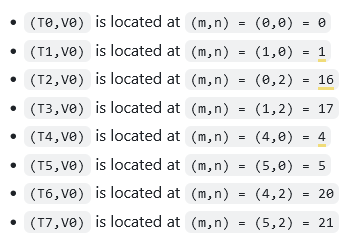
    T0V0 => ( 0,0)
    T0V1 => ( 1,0)
    T0V2 => ( 2,0)
    T0V3 => ( 3,0)
    T0V4 => (16,0)
    T0V5 => (17,0)
    T0V6 => (18,0)
    T0V7 => (19,0)
    于是改变Tile中的排布
  • M：Shape <_4,_4,_2>, Stride<_1,_8,_4>
  • N：32
  • K：4
    TiledMMA mma = make_tiled_mma(SM70_8x8x4_F32F16F16F32_NT{}, 
Layout<Shape <_2,_2>, Stride<_2,_1>>{}, // 2x2 n-major layout of Atoms 
Tile<Layout<Shape <_4,_4,_2>, Stride<_1,_8,_4>>, // Permutation on M, size 32 
_32, // Permutation on N, size 32 identity 
_4>{}); // Permutation on K, size 4 identity 
print_latex(mma);
    上面排布的改变在于更改T0V0(0,0)与T0V3(0,0)、T16V0(4,0)、T0V4(16,0)的距离
  • T0V0~T0V3：shape4、stride1
  • (T0V0~T0V3) ~ (T24V0~T24V3)：shape4(有四个这样的V0~V3的块)，stride8，这里的8就是让相邻两个块有8个跨度，T16V0距离T0V0有8个跨度
  • (T0V0~T24V3) ~ (T0V4~T24V7)：shape2，相邻只有4个跨度，那么就刚好是T0的V0到V7按顺序排列了
文章作者: WB
文章链接: https://wabbybabb0.github.io/2025/11/03/li-lun-cute/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 WB !
CUTLASS
赏
  目录