1 FlashAttention
Transformers的核心Self-attention的时间和内存的复杂度随着序列$N$增长呈$N^2$增长,很多Attention模型的目的是降低计算和内存大小,即关注FLOPS的减少并忽视了内存访问的开销。
FlashAttention使用tilling来减少在GPU显存HBM和GPU片上SRAM之间的内存读写;在backward pass时,通过存储forward pass时softmax归一化常数在片上SRAM recompute attention,FLOPS增加了,但确实实现了用更少的内存和运行速度变快。相比起传统attention减少了约9倍的HBM读写。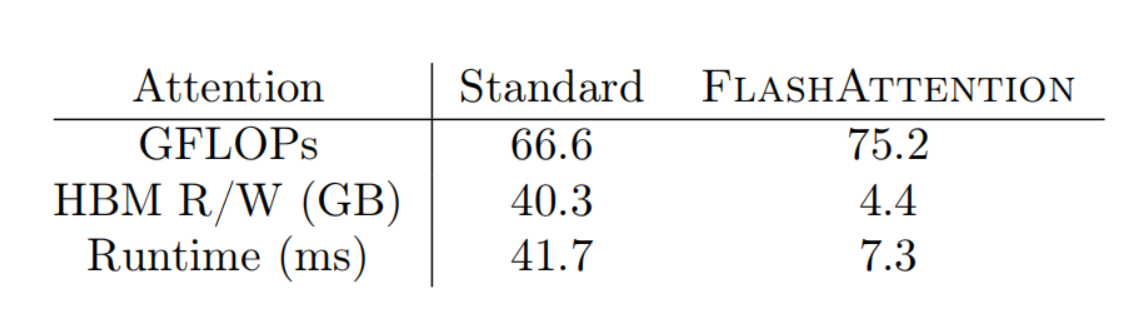
1.1 内存体系
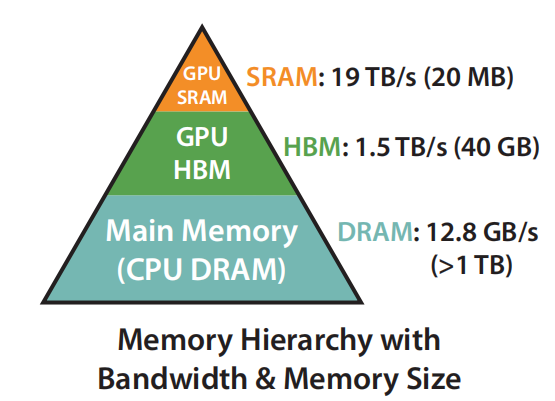
- SRAM:片上内存(缓存),分布在108个SM上,每个SM上的SRAM大小为192K,大小为20MB,读写速度19TB/s,应尽量在SRAM上存储计算中的数据。共享内存(Shared Memory)由SRAM实现。
- HBM:片下内存(显存),主要用于全局内存(Global Memory),大小为40GB,读写速度1.5TB/s。
1.2 硬件性能
GPU通过kernel(核函数)控制线程工作,每个核函数从HBM加载输入的数据,传到registers和SRAM,在片上计算完毕后将输出写回HBM。
但是随着计算相对于内存速度变得越来越快,内存速度HBM accesses成了瓶颈。在FlashAttention中,中间变量需要写回HBM保存,以便在backward pass中使用。
性能限制:
- Compute-bound:核函数运行时间主要由算数运算次数主导,如矩阵乘法,卷积
- Memory-bound:核函数运行时间主要由内存访问次数主导,如逐元素的activation、dropout和归约的sum、softmax等等。
1.3 标准Attention机制

$N$:序列长度
$d$:每个head的大小
$M$:SRAM的大小,有$d\leq M\leq Nd$
- 读取$\textbf{Q}$、$\textbf{K}$、$\textbf{V}$→$O(3Nd)$
- 读取$\textbf{S}$、$\textbf{P}$时→$O(2N^2)$
- HBM accesses→$O(Nd+N^2)$
1.4 FlashAttention
1.4.1 Tiling
- 因为softmax需要同一行的所有值才能计算,所以$QK^T$、softmax()、乘$V$分别是三个独立的算子,必须等前一环节完成后才能进行下一环。那么这就涉及三次访存和写回。
- 对于常规attention,忽略softmax和$\sqrt{d_k}$,$QK^T$得到的matrix要写回,然后又要读取出来与$V$计算,同时$N$是个比较大的值,给速度和显存带来不小的压力。
- 分块思想:可以把$qk^T$ tiling一小块的值直接和$V$进行计算,不需要访存和写回,然后进行对应位置值相加,实现小而快的效果。但是后续还是要考虑到softmax(比较重要)和d
naiveSoftmax→safeSoftmax→onlineSoftmax
- nS:如果$QK^T$的值过大,MUFU.EX2值可能会溢出。一次遍历求和,一次遍历求Attention值。

- sS:解决溢出问题,但是复杂度变高,一次遍历找最大值,一次遍历求和,一次遍历缩放+求最大值,即三次访存三次写回。

- oS:将sS求和和求最大值遍历放在一起,变成两次遍历。重点是理解第五行,一直在针对变化的max值缩放。最后需要对每个值单独做softmax,未实现显存上优化。

第六行改为$O_{j-1}\dfrac{d_{j-1}}{d_j}e^{m_{j-1}-m_j}+\dfrac{e^{x_j-m_j}}{d_j}V_j$,实现迭代地求O
Safe Softmax的提出:
如果FP16的最大表示为$2^{16}$,当$x_i=12$时,$e^{12}=162754> 2^{16}=65536$,导致数值溢出。Safe Softmax令分子分母同时缩放,$e$的幂小于0,解决数值溢出问题。
1)找出$x_1~x_N$中最大值,记为$m$,即$m=max(x_i)$
2)$softmax(\{x_1,x_2,…, x_M\})=\{\dfrac{\dfrac{e^{x_i}}{e^m}}{\sum^N_{j=1}\dfrac{e^{x_j}}{e^m}}\}^N_{i=1}=\{\dfrac{e^{x_i-m}}{\sum^N_{j=1}e^{x_j-m}}\}^N_{i=1}$
也称为softmax的max-shifting step
Softmax的Tiling:
- 合并后:
- 相当于把(分子)$f(\textbf{x}^{(1)})$、$f(\textbf{x}^{(2)})$和(分母)$\ell(\textbf{x}^{(1)})$、$\ell(\textbf{x}^{(2)})$分别都按同一个标准缩放,缩放前后$softmax$结果不变再回到下面这张图:

- 变量:
- $B_c=\lceil\dfrac{M}{4d}\rceil$,SRAM不切分$d$,$4$是指$\textbf{Q}$、$\textbf{K}$、$\textbf{V}$、$\textbf{O}$四份
- $B_r=min(\lceil\dfrac{M}{4d}\rceil,d)$,SRAM切分$N$,用$B_r$替代$N$,同时限制$\textbf{Q}$和$\textbf{O}$范围在$\mathbb{R}^{d\times d}$之内
- $\textbf{Q}$:被分成$T_r=\lceil\dfrac{N}{B_r}\rceil$个blocks$\textbf{Q}_1,…,\textbf{Q}_{T_r}$,每个block大小为$\mathbb{R}^{B_r\times d}$,$\textbf{O}$同理
- $\textbf{K}$:被分成$T_c=\lceil\dfrac{N}{B_c}\rceil$个blocks$\textbf{K}_1,…,\textbf{K}_{T_c}$,每个block大小为$\mathbb{R}^{B_c\times d}$,$\textbf{V}$同理
- $\ell$:被分成$T_r=\lceil\dfrac{N}{B_r}\rceil$个blocks$\ell_1,…\ell_{T_r}$,每个block大小为$\mathbb{R}^{B_r}$,$m$同理
- $\textbf{O}$和$\ell$的元素初始化为0,$m$初始化为$-\infty$
- 循环:
- 外层顺序计算特征
- 从HBM加载$\textbf{K}_j$和$\textbf{V}_j$到SRAM
- 内层顺序计算序列
- 从HBM加载$\textbf{Q}_i$、$\textbf{O}_i$、$\ell_{i}$、$m_i$到SRAM
- 在片上计算
- $\textbf{S}_{ij}=\textbf{Q}_i\textbf{K}_j^T\in\mathbb{R}^{B_r\times B_c}$
- $\tilde{m}_{ij}=rowmax(\textbf{S}_{ij})\in \mathbb{R}^{B_r}$,取每行的最大值
- $\tilde{\textbf{P}}_{ij}=exp(\textbf{S}_{ij}-\tilde{m}_{ij})\in \mathbb{R}^{B_r\times B_c}$,分子处理
- $\tilde{\ell}_{ij}=rowsum(\tilde{\textbf{P}}_{ij})\in\mathbb{R}^{B_r}$,分子求和得到分母
- 这一步
- $\tilde{m}_i^{new}=max(m_i,\tilde{m}_{ij})\in \mathbb{R}^{B_r}$,$m_i$是上一轮外层特征对应的rowmax,与当前的对比取新的最大值
- $\ell^{new}=e^{m_i-\tilde{m}_i^{new}}\ell_i+e^{m_i-\tilde{m}_i^{new}}\tilde{\ell}_{ij}$,$\ell_i$是上一轮外层特征对应的rowsum,更新$\ell$与当前$\tilde{m}_i^{new}$对齐
- 写回HBM的值
- $diag(\ell^{new}_i)^{-1}[diag(\ell^i)e^{m_i-\tilde{m}_i^{new}}\textbf{O}_i+e^{\tilde{m}_{ij}-m_i^{new}}\tilde{\textbf{P}}_{ij}\textbf{V}_j]$覆盖$\textbf{O}_i$
- 新$\textbf{O}_i$的rowsum:$diag(\ell^{new}_i)^{-1}$
- 新$\textbf{O}_i$的分子:之前的$\textbf{O}_i=\dfrac{分子}{diag(\ell^i)}$,所以先得到分子,再对分子按新的标准缩放;当前$\textbf{K}_j$和$\textbf{V}_j$
- $\ell^{new}_i$覆盖$\ell_i$
- $m_i^{new}$覆盖$m_i$
- $diag(\ell^{new}_i)^{-1}[diag(\ell^i)e^{m_i-\tilde{m}_i^{new}}\textbf{O}_i+e^{\tilde{m}_{ij}-m_i^{new}}\tilde{\textbf{P}}_{ij}\textbf{V}_j]$覆盖$\textbf{O}_i$
- 最后返回$\textbf{O}$
进行Forward Pass需考虑到
- 外层顺序计算特征
- softmax scaling系数$\tau$,常用的$\tau=\dfrac{1}{\sqrt{d}}$,$\textbf{S}=\tau\textbf{Q}\textbf{K}^T$
- Mask:$\textbf{S}^{masked}=MASK(\textbf{S})\in\mathbb{R}^{N\times N},\textbf{P}=softmax(\textbf{S}^{masked})$
- Drop out:$\textbf{P}^{dropped}=dropout(\textbf{P},\rho_{drop}), \textbf{O}=\textbf{P}^{dropped}\textbf{V}\in\mathbb{R}^{N\times d}$
1.4.2 Recomputation
backward pass需要$\textbf{S},\textbf{P}\in\mathbb{R}^{N\times N}$来计算梯度,FlashAttention的目标是不存储$O(N^2)$的中间变量,采用存储$\textbf{O}$和$(m,\ell)$来重新计算$\textbf{S}$和$\textbf{P}$,虽然计算量变多,但是因为HBM访问确实下降了,所以recomputation是加快了backward pass速度的。
1.4.3 Block-Sparse FlashAttention
图源李理的博客
如果$\tilde{M}_{rc}=1$,则$(\textbf{S}\cdot\mathbb{1}_{\tilde{M}})_{rc}=S_{rc}$
如果$\tilde{M}_{rc}=0$,则$(\textbf{S}\cdot\mathbb{1}_{\tilde{M}})_{rc}=-\infty$
1.5 FLOPS和IO复杂度比较
1.5.1 FLOPS复杂度
- Standard Attention
$\textbf{S}=\textbf{Q}\textbf{K}^T\in\mathbb{R}^{N\times N}$,需要$O(N^2d)$FLOPS
$\textbf{O}=\textbf{P}\textbf{V}\in\mathbb{R}^{N\times d}$,需要$O(N^2d)$FLOPS
总共FLOPS为 - FlashAttention
Theorem1
整个过程,最后得到$\textbf{O}$所需的FLOPS为$O(N^2d)$,证明如下:
- 在内层计算中,$\textbf{S}_{ij}=\textbf{Q}_i\textbf{K}_j^T\in\mathbb{R}^{B_r\times B_c}$、$\textbf{O}_i=\tilde{\textbf{P}}_{ij}\textbf{V}_j\in\mathbb{R}^{B_r\times d}$
- $\textbf{Q}_i\in\mathbb{R}^{B_r\times d}$、$\textbf{K}_j\in\mathbb{R}^{B_c\times d}$,需要$O(B_rB_cd)$FLOPS
- $\tilde{\textbf{P}}_{ij}\in\mathbb{R}^{B_r\times B_c}$、$\textbf{V}_j\in\mathbb{R}^{B_c\times d}$,需要$O(B_rB_cd)$FLOPS
- 内层循环了$T_cT_r=\lceil\dfrac{N}{B_c}\rceil\lceil\dfrac{N}{B_r}\rceil$次,因此总共FLOPS为
1.5.2 IO复杂度
Theorem2
- Standard Attention
- 第一步
- 从HBM读取$\textbf{Q}$和$\textbf{K}$,大小都为$N\times d$
- 计算$\textbf{S}=\textbf{Q}\textbf{K}^T\in\mathbb{R}^{N\times N}$写到HBM
- 显存访问$\Theta(Nd+N^2)$
- 第二步
- 计算$\textbf{P}=softmax(\textbf{S})$,需要从HBM读取$\textbf{S}$并将$\textbf{P}$写入到HBM
- 显存访问$\Theta(N^2)$
最终IO复杂度为
- FlashAttention
- 外循环:$\textbf{K}_j\in\mathbb{R}^{B_c\times d}$、$\textbf{V}_j\in\mathbb{R}^{B_c\times d}$,每个block只加载一次且大小为$B_c\times d$,所有block一共加载$T_c$次,需要$\Theta(B_cdT_c)$
- $O(B_cT_c)=N$
- 所以$\Theta(B_cdT_c)$相当于$O=(Nd)$
- 内循环:$\textbf{Q}_i\in\mathbb{R}^{B_r\times d}$、$\textbf{O}_i\in\mathbb{R}^{B_r\times d}$,每个block加载$T_c$次,大小为$B_r\times d$,所有block一共加载$T_rT_c$次,需要$\Theta(T_rT_cB_rd)$
- $O(B_rT_r)=N$
- 所以$\Theta(T_rT_cB_rd)$相当于$O(NT_cd)$
目前IO复杂度为$O(NdT_c)$
$B_c=\lceil\dfrac{M}{4d}\rceil$,$T_c=\lceil\dfrac{N}{B_c}\rceil=\lceil\dfrac{4Nd}{M}\rceil$
最终IO复杂度为这也是FlashAttention的目标,将HBM访问减小到sub-quadratic级别,即IO复杂度的增长速度小于$N^2$,大于$N$。
$d$一般为64或128,$M$大约在100KB,$M\gt\gt d^2$,$\dfrac{N^2d^2}{M}<N^2$
因此:这里是Forward Pass的IO复杂度,Backward Pass的IO复杂度与前者相同。
- Block-sparse FlashAttention
和FlashAttention的IO复杂度的计算过程比较像,不同的地方是,Block-sparse FlashAttention只需要加载非零的blocks,假设非零blocks的比例为$s$,那么HBM accesses就会被缩小到$s$倍;“However, for small values of $s$, we would still need to write the result O ∈ R 𝑁 ×𝑑 .,需要将结果$\textbf{O}\in\mathbb{R}^{N\times d}$写到HBM里”,需要的空间复杂度为:1.6 额外内存
1.6.1 Forward Pass
为了简单起见,省略了softmax时的max-shifting步骤
在计算得到$\textbf{O}\in\mathbb{R}^{N\times d}$时
$S_{ij}=q_ik_j^T$,$q_i$和$k_j$分别是$\textbf{Q}$和$\textbf{K}$的第$i$行和第$j$行,定义他们的softmax normalization常数为:
- 对于其中一个$L_i$来说,只涉及$N$个数求和,计算$L_i$所需要的额外内存的空间复杂度为:$O(N)$,通俗理解就是$1$个token对$N$个token
$v_j$是$\textbf{V}$的第$j$行,对于注意力矩阵第$i$行的输出,有 - $o_i$是第$i$个token的注意力输出,$P_{i:}\in\mathbb{R}^{1\times N}$是第$i$个token对所有其他token的softmax后的值,计算$o_i$所需要的额外内存的空间复杂度为:$O(d)$,通俗理解就是$1$个token的全部特征维度$d$
所以forward pass需要的额外内存的空间复杂度为:除了输入输出之外,还需要$O(N)$大小的空间存储$(\ell,m)$。1.6.2 Backward Pass
B.2从公式(3)后面的公式就开始看不懂了TvT…等之后再来看看吧
1.7 其他观点
Proposition3
不存在一种算法能在满足$d\leq M\leq Nd$的情况下,以$O(N^2d^2M^{-1})$次HBM accesses来计算精确注意力,证明过程如下:
如果存在$O(\dfrac{N^2d^2}{M})$,当$M=\Theta(Nd)$时,HBM accesses为$O(\dfrac{N^2d^2}{Nd})=O(Nd)$,而加载$\textbf{Q},\textbf{K},\textbf{V},\textbf{O}$时,他们的大小都是$Nd$,所以如果要精确注意力的HBM accesses,那么至少需要$\Omega(Nd)$HBM accesses,与假设相反。
1.8 实验结果

2 FlashAttention2
引用这里:FlashAttention2核心思路是尽可能减少跨不同存储层级(Memory hierarchy)的数据读写。着重于减少GMEM(对$\textbf{O}$的处理)和SMEM(见2.3)之间相互传输的数据量。
FlashAttention比标准attention的执行速度快了2-4倍,但是forward pass只用了设备的30%-50%的理论峰值FLOPs/s(见Figure 6),backward pass只用了设备的25%-35%理论峰值FLOPs/s(见Figure 7)。
相比于FlashAttention,FlashAttention2有更好的并行和任务分配机制,速度提升了两倍,在forward pass和backward pass分别达到了73%和63%的理论峰值。
相比于FasterTransformer,FlashAttention2的attention内核快了7倍。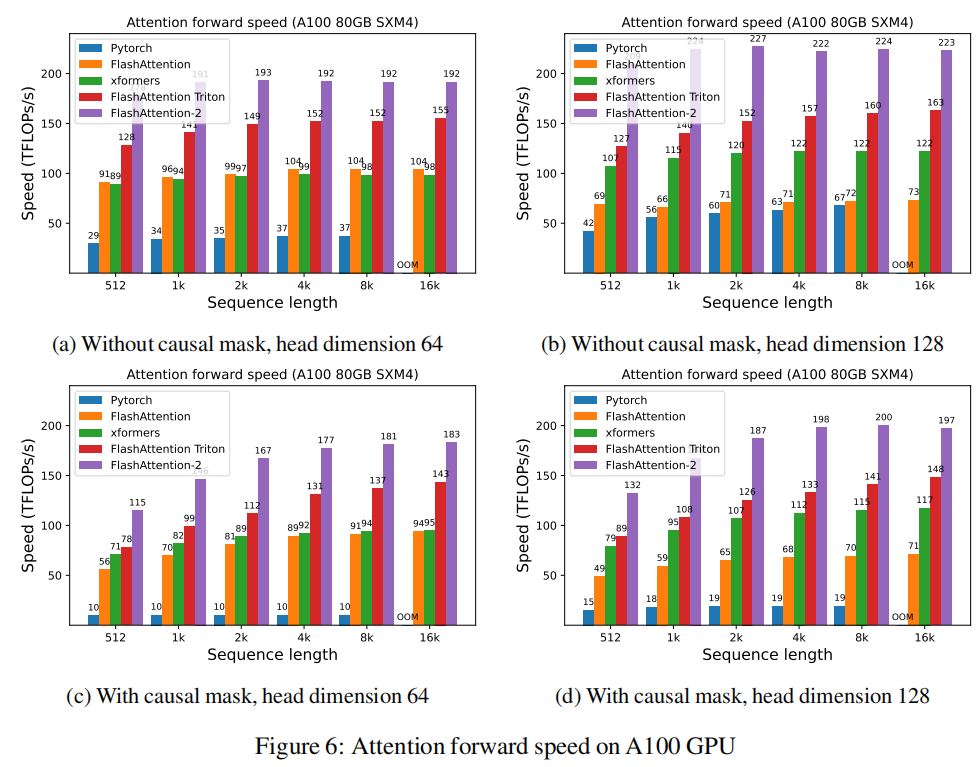
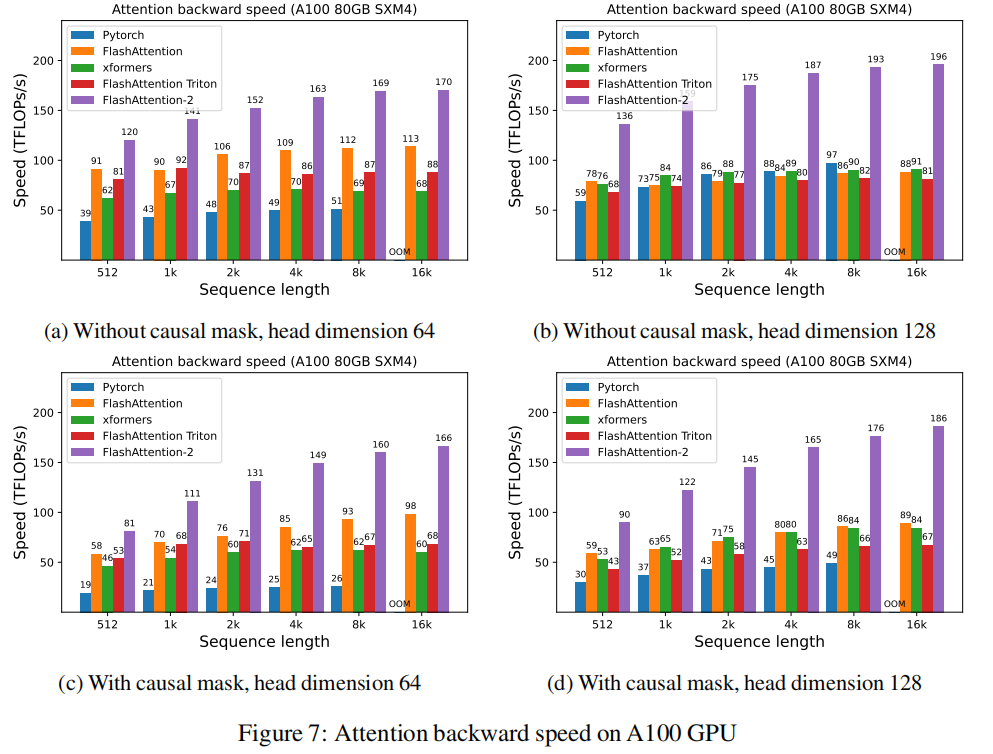
相应改进如下:
- 调整算法,在不改变输出的前提下,减少non-matmul(非矩阵乘法) FLOPs。
- 虽然non-matmul只占总FLOPs的一小部分,但是他们相比于matmul需要更长的时间(因为matmul有GPU专门的计算units)
- 在sequence lenght维度并行forward pass和backward pass,提高GPU资源的使用
- 对一个线程块的不同warps进行分工,减少通信和共享内存的读写。
2.1 算法改进
FlashAttention中,每次输出总是需要用$diag(\ell^{(current)})^{(-1)}$来rescale,FlashAttention2中,分别更新当前的$\ell^{(new)}$(即softmax的分母部分)和softmax的分子部分乘以$\textbf{V}^{(current)}$的值:同时,对于backward pass,用存储$L$代替存储$m$和$\ell$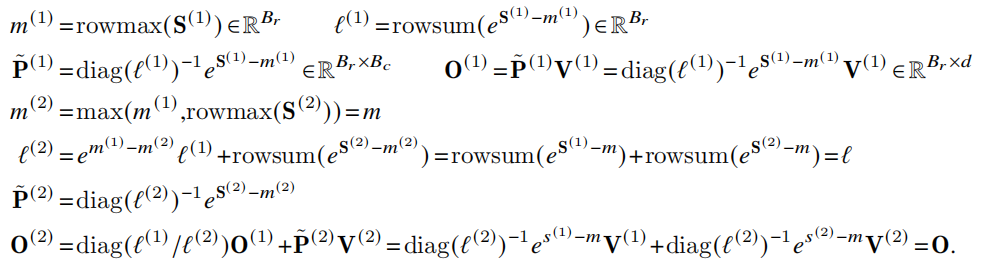
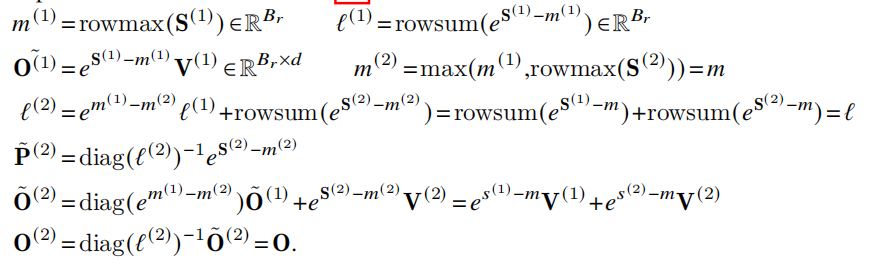
(FlashAttention2的$\tilde{\textbf{P}}^{(2)}=diag(\ell^{(2)})^{-1}e^{\textbf{S}^{(2)}-m^{(2)}}$有点奇怪,应该是$\tilde{\textbf{P}}^{(2)}=e^{\textbf{S}^{(2)}-m^{(2)}}$吧,最后再除以最新的$\ell$)
- 变量少了$m$和$\ell$并新增了一个$L$
- $L$:被分成$T_r=\lceil\dfrac{N}{B_r}\rceil$个blocks$\ell_1,…\ell_{T_r}$,每个block大小为$\mathbb{R}^{B_r}$
- $L^{(j)}=m^{(j)}+log(\ell^{(j)})$,用于backward pass使用
- 循环:
- 外层顺序计算序列
- 从HBM加载$\textbf{Q}_i$到SRAM
- 在SRAM上初始化$\textbf{Q}_i$、$\ell_i$、$m_i$
- 内层顺序计算特征
- 从HBM加载$\textbf{K}_j$、$\textbf{V}_j$到SRAM上
- 在片上计算
- $\textbf{S}_{ij}=\textbf{Q}_i\textbf{K}_j^T\in\mathbb{R}^{B_r\times B_c}$
- ${m}_i^{(j)}=max(m_i^{(j-1)},rowmax(\textbf{S}_i^{(j)})\in \mathbb{R}^{B_r}$,取当前序列上一个特征的最大值和当前特征之间的最大值作为最大值
- $\tilde{\textbf{P}}_i^{(j)}=exp(\textbf{S}_i^{(j)}-\tilde{m}_i^{(j)})\in \mathbb{R}^{B_r\times B_c}$,分子处理
- $\ell_i^{(j)}=e^{m_i^{(j-1)}-m_i^{(j)}}\ell_i^{(j-1)}+rowsum(\tilde{\textbf{P}}_i^{(j)})\in\mathbb{R}^{B_r}$,修改上一个特征的分子求和值并加上当前特征的求和值作为分母
- $\textbf{O}_i^{(j)}=diag(e^{m_i^{(j-1)}-m_i^{(j)}})\textbf{O}_i^{(j-1)}+\tilde{\textbf{P}}_i^{(j)}\textbf{V}_j$,这个只是当前序列对当前及之前的、经过softmax但是未经过归一化的”attention”值
- (内层循环完之后,也就是当前序列的attention已经有个大概的值了,但是不是最后的值,因为还没有归一化)
- 在片上计算$\textbf{O}_i=diag(\ell^{(T_c)})^{(-1)}\textbf{O}_i^{T_c}$、$L_i=m_i^{(T_c)}+\ell^{(T_c)}$
- 将$\textbf{O}_i$和$L_i$写回HBM
- 最后返回$\textbf{O}$和$L$
2.1.1 Causal masking
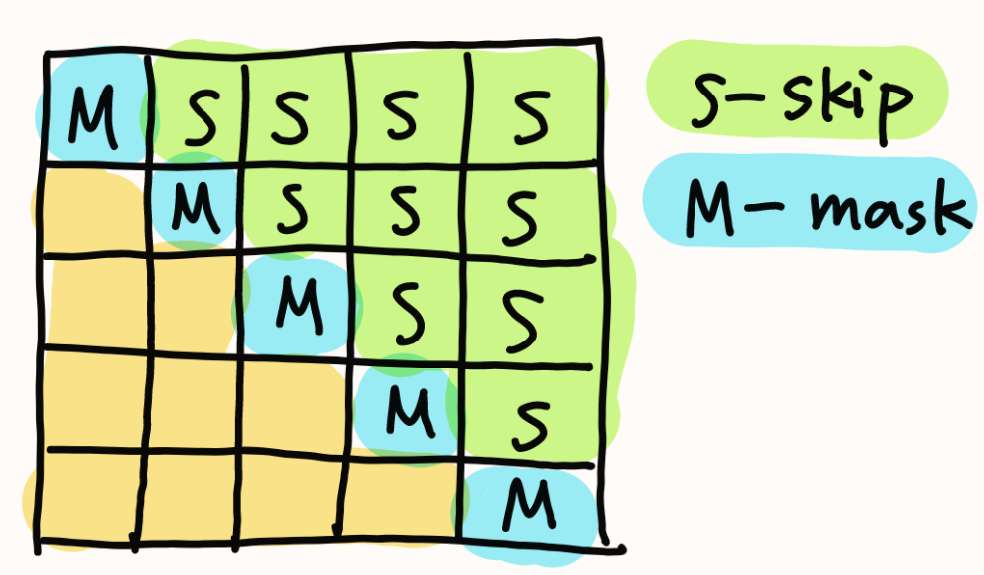
因为分块思想,对于块内所有的列索引都大于行索引的,可以直接跳过这些块的attention计算,那么每行(指块的索引)只需要有一个块是需要做casual mask的(假设每个块都是正方形)。
为什么可以肯定块内的列索引都大于行索引呢,因为从上面的公式可以保证每一个block的序列个数小于等于特征个数,也就是行索引小于等于列索引,所以可以直接用块的索引来代替原本的索引。2.1.2 计算量和内存
- 外层顺序计算序列
- 和FlashAttention一样,需要$O(N^2d)$FLOPS
- 除了输入输出之外,需要额外内存的空间复杂度为$O(N)$来存储$L$
2.2 并行
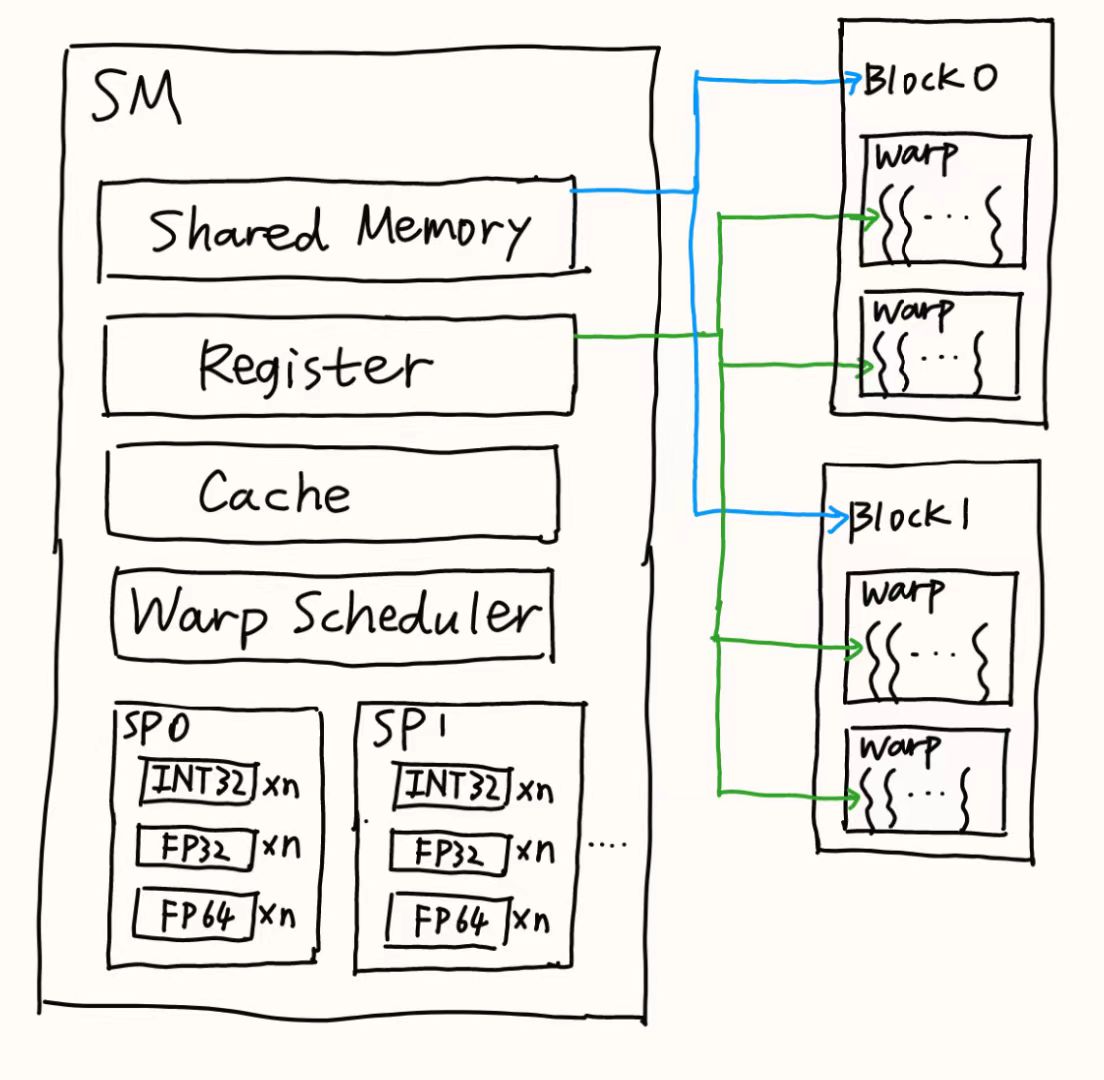
用一个线程块来处理一个attention head,因此一共有batch size × number of heads个线程块,每个线程块被安排在SM上运行。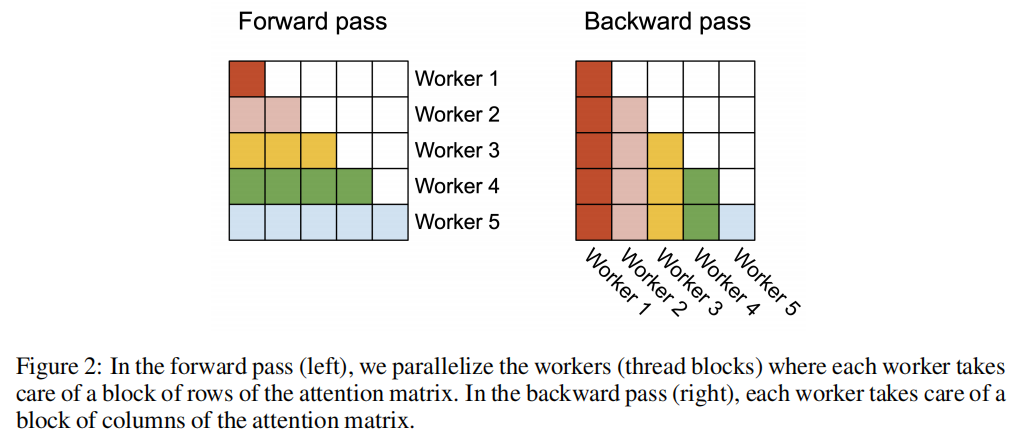
Forward Pass:并行序列长度(即外层循环)、batch维度、head维度
- 对于attention matrix,每一行block使用同一个线程块来计算,因为每个序列之间本就互相独立
Backward Pass:只需要在不同的列blocks更新$\textbf{dQ}_i←\textbf{dQ}_i+\textbf{dS}_i^{(j)}\textbf{K}_j$ - 对于attention matrix,每一列block使用同一个线程块来计算,然后再读不同线程块的结果相加来更新$\textbf{dQ}$(行方向)

2.2.1 Decoding
- 在训练或者预填充时Attention的瓶颈为中间矩阵($\textbf{Q}\textbf{K}^T$和$softmax(\textbf{Q}\textbf{K}^T)$)的读写。
- 在Decoding阶段,因为是对新的token进行attention,只有它需要与之前的tokens的KV需要互动,所以query length很短,通常为1。于是Attention的瓶颈变为了加载KV cache的速度。
- 在不同线程块之间切分KV cache的加载来增加HBM宽带的占用率,但是线程块之间的通信不算很快。
- 最后采取将中间结果写入HBM,然后调用一个单独的kernel来归约并产生最终输出。
2.3 warps的分工
给线程块分配4或8个warps
Forward pass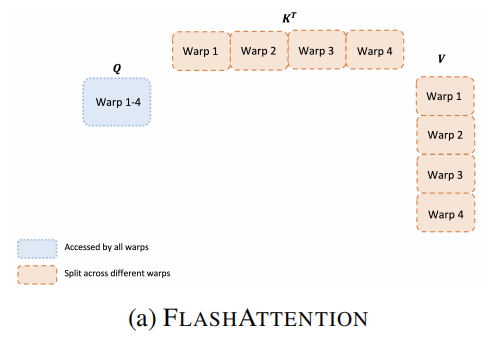
FlashAttention将$\textbf{K}$和$\textbf{V}$切分到4个warps中,同时所有warps可以访问$\textbf{Q}$。
每个warp进行计算得到一部分$\textbf{Q}\textbf{K}^T$,再乘对应部分的$\textbf{V}$,然后再相加。
这种”split-K”方案方法需要将两次得到的部分结果都写到shared memory里让不同的warps共享才能进行相加,这增加的读写量降低了forward pass的速度。(在2.2“SM和线程块的关系”一图中,每个线程块的shared memory是线程块内部共享的)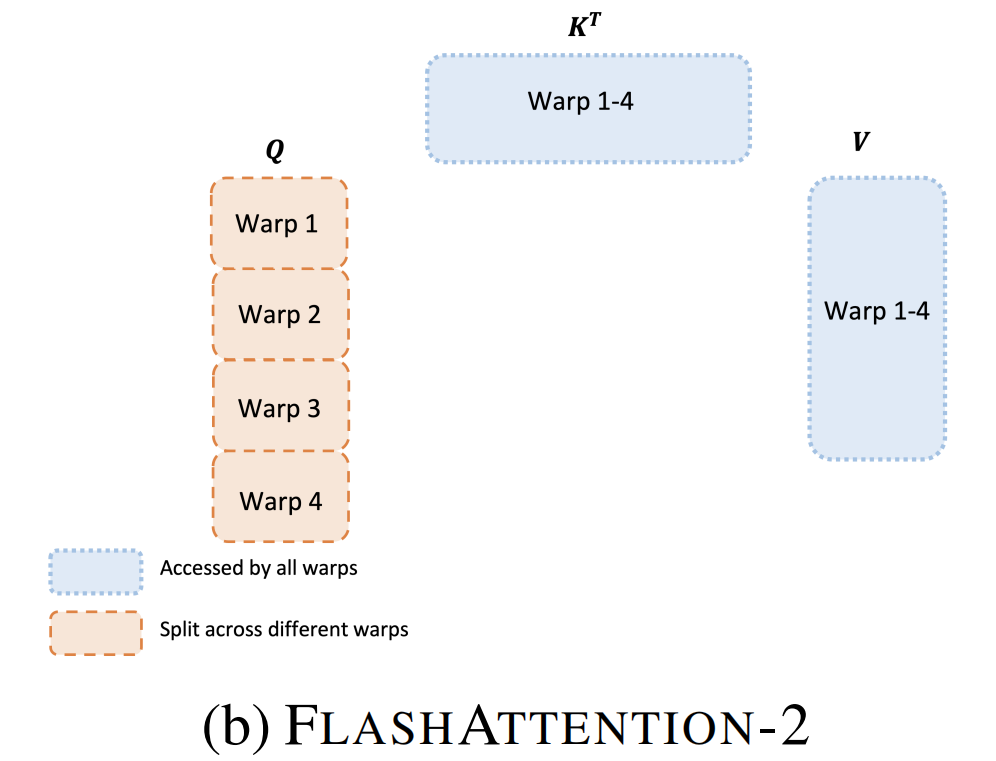
- FlashAttention2将将$\textbf{Q}$切分到4个warps中,同时所有warps可以访问$\textbf{K}$和$\textbf{V}$,同样的,每个warp进行计算得到一部分$\textbf{Q}\textbf{K}^T$,再乘对应部分的$\textbf{V}$,然后再相加。这里的中间结果是在当前warp下的,不需要进行warps之间的数据传递,因此不需要共享内存读写并能提升速度。
Backward pass
过程中,因为$\textbf{Q}$、$\textbf{K}$、$\textbf{V}$、$\textbf{O}$、$\textbf{dQ}$、$\textbf{dK}$、$\textbf{dV}$之间是存在依赖关系的,需要一些同步,不像$\textbf{Q}_i$之间互相独立,但不使用”split-K”还是可以减少一些共享内存的读写并提升速度。
Tuning block sizes
线程块增大可以减少shared memory的读写,但是增加了所需的resigter和总的shared memory。最后FlashAttention2选择线程块大小为$\{64, 128\}\times\{64, 128\}$,(4种选择的)最终取决于head的大小$d$和设备的shared meomory大小。
3 FlashAttention3
Flash Attention 3 深度解析:与其说FA3是FA2算法改进的延续,不如说FA3的工程创新是如何充分发挥Hopper架构强大算力的说明书。理解了FA3的原理,就相当于理解了Hopper硬件架构的特性和针对新架构做性能优化的一系列方案。
在了解FlashAttention3之前,最好先看以下内容:
Nvidia Hopper WGMMA计算分析
Hopper-100架构
回顾一下,FlashAttention用tiling和recompute方法,在一个单独的GPUkernels上通过融合attention的操作,减少会使GMEM变慢的中间过程的IO读写;FlashAttention2更改FlashAttention对特征并行计算的算法,改为对序列并行计算,改善GPU的占用和分配问题。
但是,FlashAttenion2在H100的GPU利用率低,只有35%,相比于优化后的GEMM80~90%的使用率,显得非常逊色。原因是它遵循简单的同步机制,没有利用H100的异步和低精度特性。所以FlashAttention3的提出就是为了利用H100架构的DAS化特性。
- H100有异步机制单元Tensor Cores WGMMA,TMA,可以让数据搬运和计算重叠。
- TMA:Tensor Memory Accelerator,内存搬运加速
- WGMMA:warpgroup MMA,线程束级别MMA
- 低精度
FlashAttention3的升级在于根据Hopper架构来改进其算法。
- FP16:在forward pass中,FlashAttention3比FlashAttention2提升了1.5-2倍速度(达到740TFLOPSs/s),backward pass提升了1.5-1.75倍
- FP8:
FlashAtttention3新特征:
H100新特性:
- WGMMA:意味着有更高的吞吐,通过一个warpgroup执行(即4个连续的warps)
- 用WGMMA代替MMA
mma.sync是A卡指令,只能达到吞吐量峰值的2/3
- TMA:意味着更快的GMEM到SMEM数据传输,可以异步执行
- 相比CPA,减少了使用寄存器进行地址计算
- FA2用CPA从GMEM加载tile
这两个新特性自然地集成到producer warp和consumer warp的pipeline设计中
- Producer-Consumer异步机制:对warpgroup设置不同任务,分为producer warpgroup和consumer warpgroup,异步执行数据移搬运和Tensor Cores计算,隐藏内存和指令延迟。
- 在异步blocks级别GEMM(即WGMMA)下隐藏softmax:softmax中floating乘加和指数计算都是低吞吐的non-GEMM操作,而GEMM操作的吞吐量较高,通过异步指令WGMMA实现计算重叠,具体分为inter warpgroup和intra warpgroup,在FlashAttention2的基础上做到规避softmax和GEMM的依赖关系,隐藏softmax造成的一部分延迟。
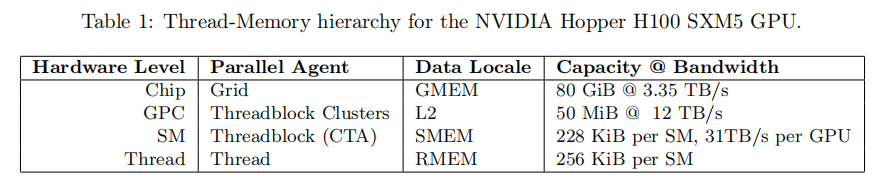
3.1 GPU架构特征和执行模型
3.1.1 内存体系和线程体系
H100的
内存体系:
- GMEM是可以访问全部SMs的片下DRAM,其物理实现依靠HBM
- 在GMEM的数据缓存在片上的L2 cache中
- 每个SM包含一个小型片上存储缓存SMEM
- 每个SM都有寄存器堆
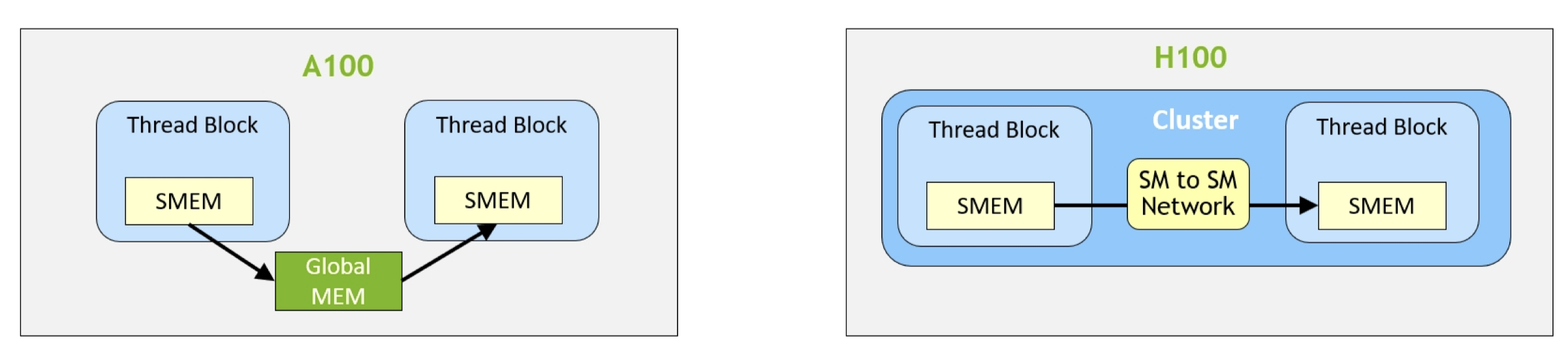
线程体系: - GPU编程模型是在线程上按逻辑组织运行的,从小到大的线程组织包括:线程threads、线程束warps(32个线程)、warpsgroups(4个连续的warps)、线程块threadblocks(i.e. cooperative thread arrays or CTAs)、threadblock clusters(Hopper架构的)、网格grids
这两种体系的关系: - 同一threadblocks中的threads被共同调度在同一SM上,线程只能访问所属线程块的SMEM,每个threads最多有256个RMEM
- 同一threadblock clusters中的threadblocks被共同调度在同一GPC上,线程可访问clusters内的SMEM
3.1.2 异步和warp-specialization
- warp-specialized的异步机制:在同一个threadblock的warps会被分为producer或者consumer,只解决数据移动或者计算。
- 数据搬运:TMA硬件单元支持GMEM和SMEM之间异步内存拷贝,将数据从GMEM搬运到SMEM,搬运完成后TMA通知consumer,同时等待SMEM buffer释放。
- 计算:通过WGMMA指令,实现Tensor Core异步,直接从SMEM中获取输入,计算GEMM和softmax,释放buffer并通知producer。
- Hopper支持通过
setmaxnreg动态重新分配warpgroups的register,因此做MMA的warps(即consumer,相比于producer工作量大)可以获得更大的RMEM,数据搬运的RMEM就会少一些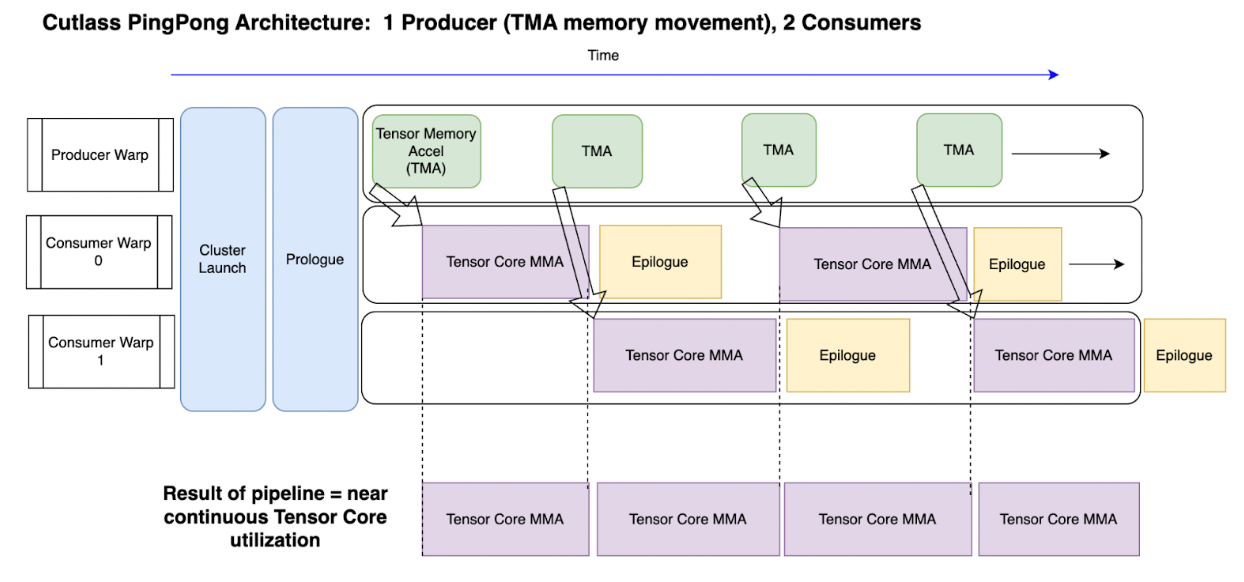
3.1.3 低精度格式
这部分Flash Attention 3 深度解析讲解得很好
两个问题: - FP8 WGMMA要求必须要在最内层维度上连续(k-major),即A行连续,B列连续,两种思路:
- QKV都是行连续,P也是行连续,需要V做转置
- QKV通常是BHSD,而P是BHSS,需要在seq len维度上连续,而V的最后一个维度是head dim,于是需要对V的S和D维度做transpose
- 解决:使用LDSM/STSM
- FP32 WGMMA accumulater(即C)寄存器的排列布局与FP8 WGMMA A的不同
- warp-specialization
FlashAttention3的forward pass和FlashAttention2一样,在batch size、number of heads和$Q$的序列长度进行并行,因此一个CTA-level级的算法是可以应对前面的并行的,具体做法是将$\textbf{Q}$分块。
- 个人理解:$\textbf{Q}$是tiling思想,threadblocks其实也是tiling思想,将线程分块。然后每个线程划分为两个线程束的集合,即producer warpgroup和consumer warpgroup,也是继承了tiling,二者是异步关系
- CTA-view:
- producer:将数据从GMEM加载到SMEM
- 就是FA2+TMA&WGMMA的warp specialization

- 初始化一个pipeline对象,管理barrier synchronization使各个线程之间同步协调,使用一个s-stage的循环SMEM buffer。
- 如果当前thread所在的warpgroup属于producer(处理数据移动)
- 释放一部分registers
- 把当前分块$\textbf{Q}_i$从HBM加载到SMEM
- 加载完成后,通知属于consumer的threads加载$\textbf{Q}_i$
- 遍历$T_c$个$\textbf{K}$和$\textbf{V}$的分块
- 等待当前循环buffer的第$j\%s$阶段被consumer使用完,防止旧数据未利用完就加载新数据将旧数据覆盖
- 把当前分块$\textbf{K}_j$和$\textbf{V}_j$从HBM加载到SMEM,对应循环buffer的第$j\%s$阶段
- 加载完成后,通知属于consumer的threads加载$\textbf{K}_j$和$\textbf{V}_j$
如果当前thread所在的warpgroup属于consumer(处理计算)
- 根据consumer warps的数量重新分配registers
- 在片上初始化$textbf{Q}_i$、$\ell_i$、$m_i$
- 等待$\textbf{Q}_i$加载到SMEM
- 遍历$T_c$个$\textbf{K}$和$\textbf{V}$的分块
- 等待$\textbf{K}_j$加载到SMEM
- SS-GEMM(数据来源都是SMEM):计算$\textbf{S}_i^{(j)}=\textbf{Q}_i\textbf{K}_j^T$
- 存储$m_i^{old}=m_i$,更新$m_i=max(m_i^{old},rowmax(S_i^{(j)}))$
- 计算$\tilde{\textbf{P}}_i^{(j)}=exp(\textbf{S}_i^{(j)}-m_i)$和$\ell_i=exp(m_i^{old}-m_i)\ell_i+rowmsum(\tilde{\textbf{P}}_i^{(j)})$
- 等待$\textbf{V}_j$加载到SMEM
- RS-GEMM($\tilde{\textbf{P}}_i^{(j)}$在RMEM中,$\textbf{V}_j$在SMEM中):计算$\textbf{O}_i=diag(exp(m_i^{old}-m_i))^{-1}\textbf{O}_i+\tilde{\textbf{P}}_i^{(j)}\textbf{V}_j$
- 释放第$j\%s$阶段的buffer给producer使用
- 最后根据最新的$\ell_i$计算$\textbf{O}_i=diag(\ell_i)^{-1}\textbf{O}_i$和$L_i=m_i+log(\ell_i)$
- 将$\textbf{O}_i$和$L_i$写回HBM作为第$i$个分块的$\textbf{O}$和$L$
setmaxnreg负责释放register
- TMA负责加载$\textbf{Q}_i$和$\{\textbf{K},\textbf{V}\}_{0\leq j\leq T_c}$,TMA加载是并行的,因为异步的关系,不会在其他加载完成时互相阻塞。
- 用WGMMA指令在consumer主循环中执行GEMMs。
- pingpong scheduling
为什么要把GEMM和softmax的计算重叠?
- softmax的计算包括指数计算,是non-matmul计算,吞吐量比matmul的要少得多,计算non-matmul用时也占据不小的一部分
- 例如,M=128、M=128、K=192,计算$QK^T$时
- WGMMA计算量为$2\times128\times192\times128=6291456FLOPS$,WGMMA吞吐为$2048FLOPS/cycle$,计算得到延迟$=3072cycles$
- MUFU.EX2计算量为$192\times128=24576OPS$,exp吞吐为$16OPS/cycle$,计算得到延迟=$1536cycles$
- softmax里exp的吞吐和WGMMA的吞吐相差太多,延迟是tensor core的一半,如果让tensor core等待exp计算会非常不划算,于是采用计算重叠的方式,用算力高的tensor core保持busy状态掩盖算力低的cuda core
- FP8的情况会给你更糟糕,WGMMA和EX2都是1536cycles
Inter warpgroup——Warp-Specialized Persistent Ping-Pong kernel design
warpScheduler,每个warpgroup有128个线程,这刚好是在一个SM上一个线程块的大小
- synchronization barries令warpgroup 1的GEMMs运行在warpgroup 2的GEMMs之前。其中GEMMs包括GEMM1和GEMM0,分别是当前轮的$\textbf{P}\textbf{V}$和下一轮的$\textbf{Q}\textbf{K}^T$
- 然后warpgroup 1执行softmax,warpgroup 2执行GEMMs(GEMM1和GEMM0)
- 然后warpgroup 1执行GEMMs(GEMM1和GEMM0),warpgroup 2执行softmax

实际上,CTA-level的任务是由tile scheduler分配的,可以安排block或warpgroup计算某个tile。当在tensor core执行matmul时,exp的计算通过synchronization barries(bar.sync指令),由cuda core异步执行。在warpgroup-level的调度和barries的共同控制下,同一gemm的不同output tile可以在两个warpgroup之间丝滑的切换,就如Ping-Pong内核流水线,持续向tensor core输送数据,实现或接近其最大算力。
对于其他attention变体如MQA和GQA,仍然采取FlashAttention2的算法,避免在HBM重复加载$\textbf{K}$和$\textbf{V}$
3.2.2 warpgroup内部GEMMs和softmax的重叠
Intra warpgroup
GEMM1:$\textbf{P}\textbf{V}$
GEMM0:$\textbf{Q}\textbf{K}^T$
为什么要考虑到内部的重叠?
- tensor core的执行粒度是gemm,如果要让tensor core保持busy状态,在warpgroup内部也要用WGMMA掩盖softmax的计算。根据GEMM1依赖softmax的输出,softmax依赖GEMM0的输出的关系,我们希望可以做到在进行GEMM0的WGMMA0后立马执行GEMM1的WGMMA1
- 如果要实现busy状态,就不能再顺序地完整执行i-th iteration后再执行i+1-th。又因为tensor core的异步关系,通过滞后计算GEMM1达到掩盖softmax计算的效果,如下图所示,让i+1-th的GEMM0和i-th的GEMM1在i+1-th的softmax时进行衔接。
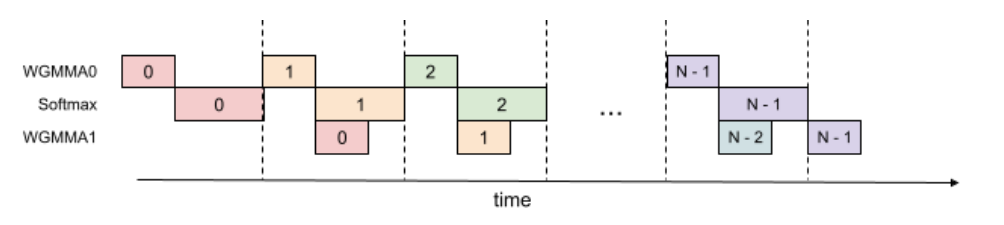
虽然记录i-th的中间结果会增加寄存器的使用,但是TFLOPs确实增加了
考虑intra-warpgroup后的算法
- 第11~13行实现掩盖softmax
随记
Persistent Kernel:
启动固定数量的CTAs来占用整个GPU,可以为CTAs分配多个工作块,提高SM使用率
- 没有persistent kernel:每个CTA对应一个work tile,当tile工作量不太均匀时,会导致SMs空闲
- 有persistent kernel:在 H100 SXM5 GPU 上,有132个SMs,每个SM负责一个CTA,一个CTA动态处理work tiles(一对多)。在causal masking的时候可以动态调度work tile。可以在前一个tile的收尾阶段预加载下一个tile,实际上掩盖了没有persistent kernel时同一个SM在两个CTA之间切换的延迟。
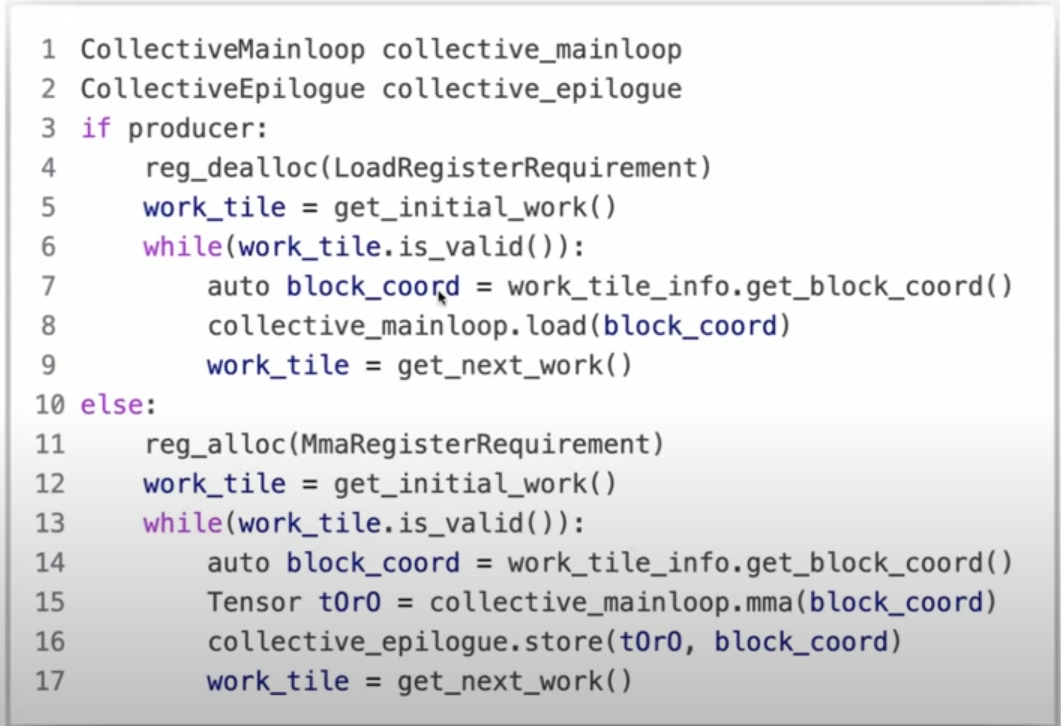
t0r0:thread-wise accumulator of attention output
t代表thread-level,r表示register



