高性能计算

发布日期: 2025-03-19

更新日期: 2025-03-26

文章字数: 3.7k

阅读次数:

DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model

本文内容围绕多头注意力机制的演变过程，着重记录MLA的设计原理，对缓存与效果的极限拉扯：从MHA、MQA、GQA到MLA、DeepSeek-v2 MLA 原理讲解的内容进行整合与分析，在我理解MLA的过程中，他们给予了很好的启迪！

假设所有输入都为行向量，输入序列为$\textbf{x}_1, \textbf{x}_2, …, \textbf{x}_l$，其中$\textbf{x}_i\in \mathbb{R}^{1\times d}$

$l$：token数量
$d$：embdeding dimension

1 MHA(Multi Head Attention)

$\textbf{o}_t=[\textbf{o}_t^{(1)}, \textbf{o}_t^{(2)}, ..., \textbf{o}_t^{(h)}]$

$\textbf{o}_t$：当前token的注意力输出 $\textbf{o}_t^{(s)} = Attention(\textbf{q}_t^{(s)}, \textbf{k}_{i\leq t}^{(s)}, \textbf{v}_{i\leq t}^{(s)}) = \sum^t_{i=1}softmax(\dfrac{\textbf{q}_t^{(s)}\textbf{k}_i^{(s)T}}{\sqrt{d_k}})\textbf{v}_i^{(s)}$
$\textbf{o}_t^{(s)}$：当前token的第$s$个head的注意力输出，$h$ 个head拼接得到$O_t$，其中： $\textbf{q}_i^{(s)}=\textbf{x}_i\textbf{W}_q^{(s)}\in \mathbb{R}^{1\times d_k},\ \ \ \ \ \textbf{W}_q^{(s)}\in \mathbb{R}^{d\times d_k}$ $\textbf{k}_i^{(s)}=\textbf{x}_i\textbf{W}_k^{(s)}\in \mathbb{R}^{1\times d_k},\ \ \ \ \ \textbf{W}_k^{(s)}\in \mathbb{R}^{d\times d_k}$ $\textbf{v}_i^{(s)}=\textbf{x}_i\textbf{W}_v^{(s)}\in \mathbb{R}^{1\times d_v},\ \ \ \ \ \textbf{W}_v^{(s)}\in \mathbb{R}^{d\times d_v}$
$\textbf{W}_q^{(s)}$、$\textbf{W}_k^{(s)}$、$\textbf{W}_v^{(s)}$：分别为第$s$个head的query、key、value的权重矩阵，
$d_k=d_v=d/h$

MHA使每个Head都有对应的$K$和$V$，模型对token的理解效果是比较好的，而问题在于，虽然有KV Cache，但是随着句子序列变长，Key和Value的缓存的成本和推理时通信的短板会变大，下图的解释会更详细点。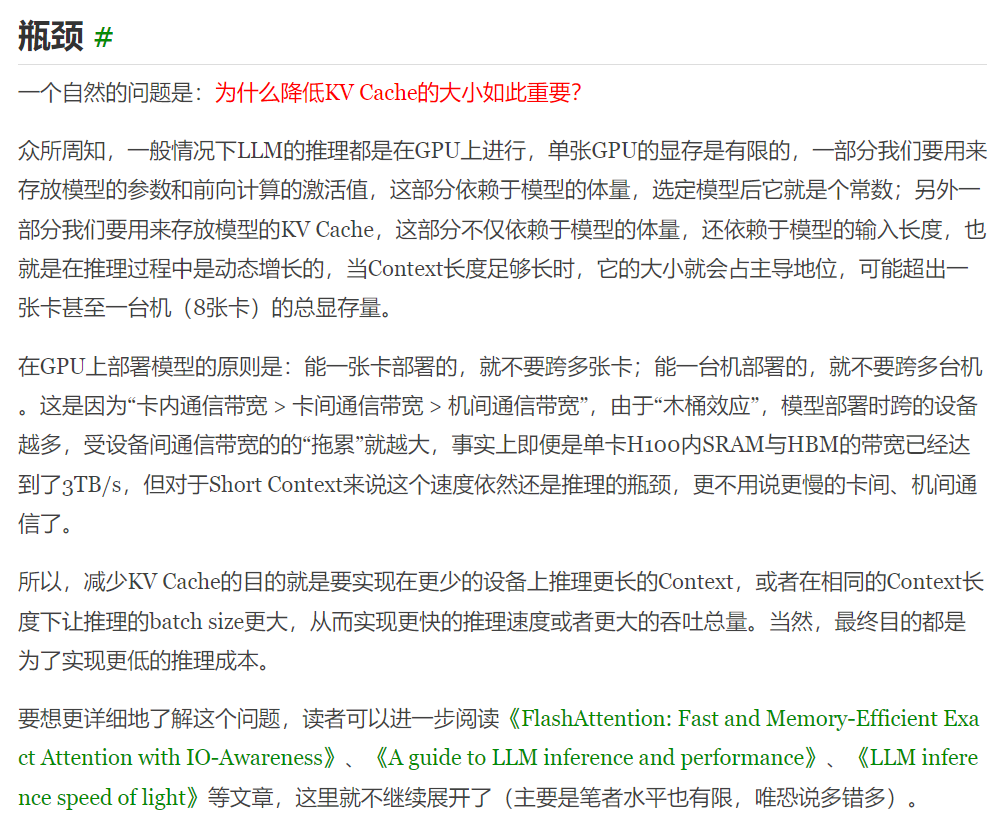
《缓存与效果的极限拉扯：从MHA、MQA、GQA到MLA》一文中对KV Cache的分析

2 MQA(Multi Query Attention)

$\textbf{o}_t=[\textbf{o}_t^{(1)}, \textbf{o}_t^{(2)}, ..., \textbf{o}_t^{(h)}]$ $\textbf{o}_t^{(s)} = Attention(\textbf{q}_t^{(s)}, \textbf{k}_{i\leq t}, \textbf{v}_{i\leq t}) = \sum^t_{i=1}softmax(\dfrac{\textbf{q}_t^{(s)}\textbf{k}_i^T}{\sqrt{d_k}})\textbf{v}_i$ $\textbf{q}_i^{(s)}=\textbf{x}_i\textbf{W}_q^{(s)}\in \mathbb{R}^{1\times d_k},\ \ \ \ \ \textbf{W}_q^{(s)}\in \mathbb{R}^{d\times d_k}$ $\textbf{k}_i=\textbf{x}_i\textbf{W}_k\in \mathbb{R}^{1\times d_k},\ \ \ \ \ \textbf{W}_k\in \mathbb{R}^{d\times d_k}$ $\textbf{v}_i=\textbf{x}_i\textbf{W}_q\in \mathbb{R}^{1\times d_v},\ \ \ \ \ \textbf{W}_v\in \mathbb{R}^{d\times d_v}$

$\textbf{W}_k$、$\textbf{W}_v$：所有head共享的key、value权重矩阵

与MHA相比，每个Head都共享同一组$K$和$V$，

显存：其KV Cache为MHA的$\dfrac{1}{h}$，是目前很节省的方法，
效果：根据《缓存与效果的极限拉扯：从MHA、MQA、GQA到MLA》提到的，损失是有限的，参数量通过加大其他模块的规模来补足。

3 GQA(Grouped Query Attention)

$\textbf{o}_t=[\textbf{o}_t^{(1)}, \textbf{o}_t^{(2)}, ..., \textbf{o}_t^{(h)}]$ $\textbf{o}_t^{(s)} = Attention(\textbf{q}_t^{(s)}, \textbf{k}_{i\leq t}^{(\lceil sg/h \rceil)}, \textbf{v}_{i\leq t}^{(\lceil sg/h \rceil)}) = \sum^t_{i=1}softmax(\dfrac{\textbf{q}_t^{(s)}\textbf{k}_i^{(\lceil sg/h \rceil)}T}{\sqrt{d_k}})\textbf{v}_i^{(\lceil sg/h \rceil)}$ $\textbf{q}_i^{(s)}=\textbf{x}_i\textbf{W}_q^{(s)}\in \mathbb{R}^{1\times d_k},\ \ \ \ \ \textbf{W}_q^{(s)}\in \mathbb{R}^{d\times d_k}$ $\textbf{k}_i^{(\lceil sg/h \rceil)}=\textbf{x}_i\textbf{W}_k^{(\lceil sg/h \rceil)}\in \mathbb{R}^{1\times d_k},\ \ \ \ \ \textbf{W}_k^{(\lceil sg/h \rceil)}\in \mathbb{R}^{d\times d_k}$ $\textbf{v}_i^{(\lceil sg/h \rceil)}=\textbf{x}_i\textbf{W}_q^{(\lceil sg/h \rceil)}\in \mathbb{R}^{1\times d_v},\ \ \ \ \ \textbf{W}_v^{(\lceil sg/h \rceil)}\in \mathbb{R}^{d\times d_v}$

$\lceil · \rceil$是向上取整
$\textbf{W}_q^{(s)}$、$\textbf{W}_k^{(s)}$、$\textbf{W}_v^{(s)}$：分别为第$s$个head的query、key、value的权重矩阵，
$d_k=d_v=d/h$

作为显存的压缩和效果都在MHA和MQA之间的版本，GQA将head分为$g$个组($g$可以整除$h$)，每组共享同一对$K$、$V$。当$g=1$时就是MQA，$g=h$时就是MHA。当$1<g<h$时，效果不如MHA，显存压缩没有MQA那么猛，但是KV Cache压缩到MHA的$g/h$，效果比MQA好，是一个折中的版本。

4 MLA(Multi-head Latent Attention)

对KV Cache做低秩投影，通过投影矩阵$\textbf{W}_c$将$\textbf{x}_i$投影为$\textbf{c}_i$
缓存与效果的极限拉扯：从MHA、MQA、GQA到MLA文章中认为”DeepSeek-V2的技术报告里是从低秩投影的角度引入MLA的……然而，笔者认为低秩投影这个角度并不贴近本质，因为要说低秩投影的话，事实上只要我们将GQA的所有K、V叠在一起，就会发现GQA也相当于在做低秩投影：

$[\textbf{k}_i^{(1)}, ...,\textbf{k}_i^{(g)}, \textbf{v}_i^{(1)},...,\textbf{v}_i^{(g)}] = \textbf{x}_i[\textbf{W}_k^{(1)},...,\textbf{W}_k^{(g)},\textbf{W}_v^{(1)},...,\textbf{W}_v^{(g)}]$

$[\textbf{k}_i^{(1)}, …,\textbf{k}_i^{(g)}, \textbf{v}_i^{(1)},…,\textbf{v}_i^{(g)}] = \textbf{c}_i\in \mathbb{R}^{1\times d_c}$，将所有的$\textbf{k}_i^{(s)}$、$\textbf{v}_i^{(s)}$拼在一起记为$\textbf{c}_i$，
$[\textbf{W}_k^{(1)},…,\textbf{W}_k^{(g)},\textbf{W}_v^{(1)},…,\textbf{W}_v^{(g)}] = \textbf{W}_c\in \mathbb{R}^{d\times d_c}$，将相应的投影矩阵拼在一起记为$\textbf{W}_c$，
$d_c=g(d_k+d_v)<d=h(d_k+d_v)$，所以$\textbf{x}_i$到$\textbf{c}_i$的变换就是一个低秩投影，
所以，MLA的本质改进不是低秩投影，而是低秩投影之后的工作“

4.1 MLA的最初构想

得到$\textbf{c}_i$后，GQA将其对半分为K和V，将它们分别均分为$g$份，每一份复制$h/g$次，凑够$h$份K和V，然后将其投入到计算Attention和KV Cache，MLA对$\textbf{c}_i$不是简单的分割和复制，他对$\textbf{c}_i$又进行了一次投影，“增强了模型的能力”：

$\textbf{u}_t = \textbf{o}_t\textbf{W}_o,\ \ \ \ \ \textbf{W}_o\in \mathbb{R}^{d\times hd_k}$

$\textbf{W}_o$是输出投影矩阵，这里的$hd_k\neq d$ $\textbf{o}_t=[\textbf{o}_t^{(1)}, \textbf{o}_t^{(2)}, ..., \textbf{o}_t^{(h)}] \in \mathbb{R}^{1\times d}$ $\textbf{o}_t^{(s)} = Attention(\textbf{q}_t^{(s)}, \textbf{k}_{i\leq t}^{(s)}, \textbf{v}_{i\leq t}^{(s)}) = \sum^t_{i=1}softmax(\dfrac{\textbf{q}_t^{(s)}\textbf{k}_i^{(s)T}}{\sqrt{d_k}})\textbf{v}_i^{(s)}$ $\textbf{c}_i=\textbf{x}_i\textbf{W}_c\in\mathbb{R}^{1\times d_c}$ $\textbf{q}_i^{(s)}=\textbf{x}_i\textbf{W}_q^{(s)}\in \mathbb{R}^{1\times d_k},\ \ \ \ \ \textbf{W}_q^{(s)}\in \mathbb{R}^{d\times d_k}$ $\textbf{k}_i^{(s)}=\textbf{c}_i\textbf{W}_{Uk}^{(s)}\in \mathbb{R}^{1\times d_k},\ \ \ \ \ \textbf{W}_{Uk}^{(s)}\in \mathbb{R}^{d_c\times d_k}$ $\textbf{v}_i^{(s)}=\textbf{c}_i\textbf{W}_{Uv}^{(s)}\in \mathbb{R}^{1\times d_v},\ \ \ \ \ \textbf{W}_{Uv}^{(s)}\in \mathbb{R}^{d_c\times d_v}$
$\textbf{W}_{Uk}^{(s)}$、$\textbf{W}_{Uv}^{(s)}$：分别为第$s$个head的key、value的再投影权重矩阵，为了“增强了模型的能力”
然而，原本已经低秩的$\textbf{c}_i$在$\textbf{W}_{Uk}^{(s)}$和$\textbf{W}_{Uv}^{(s)}$作用下被up-projection了，即$\textbf{k}_i^{(s)}$和$\textbf{v}_i^{(s)}$原本的head分组不存在了，一组head之间不再共享$K$、$V$，“出于节省计算和通信成本的考虑，我们一般会缓存的是投影后的$\textbf{k}_i$、$\textbf{v}_i$的而不是投影前的$\textbf{c}_i$或$\textbf{x}_i$”，所以，此做法的KV Cache与MHA无异，没有显存节省的作用。

虽然在训练阶段MLA的优化空间不大，但是在推理阶段中：

$\textbf{q}_t^{(s)}\textbf{k}_i^{(s)T}=(\textbf{x}_t\textbf{W}_q^{(s)})\cdot (\textbf{c}_i\textbf{W}_{Uk}^{(s)})^T=\textbf{x}_t(\textbf{W}_q^{(s)}\cdot\textbf{W}_{Uk}^{(s)T})\textbf{c}_i^T$

$\textbf{W}_q^{(s)}\cdot\textbf{W}_{Uk}^{(s)T}$作为$Q$的投影矩阵，K Cache的内容可以从$\textbf{k}_i$变为$\textbf{c}_i$；根据$\textbf{v}_i^{(s)}=\textbf{c}_i\textbf{W}_{Uv}^{(s)}$和$\textbf{u}_t^{(s)} = \textbf{o}_t^{(s)}\textbf{W}_o^{(s)}$，输出的计算过程包含$\textbf{c}_i\textbf{W}_{Uv}\textbf{W}_O$，那么$\textbf{W}_{Uv}\textbf{W}_O$作为$V$的投影矩阵，$\textbf{v}_i$可以用$\textbf{c}_i$代替，即V Cache的内容从$\textbf{v}_i$也变为$\textbf{c}_i$。
那么KV Cache的内容就是$\textbf{c}_i$，它与$(s)$无关，是所有head共享的，控制好$g/h$的值，在推理阶段达到GQA或MQA的效果。
实际上，因为up-projection提高了模型的效果，同时在推理阶段KV Cache效果与GQA相同($1<g<h$)。在效果和显存的平衡下，“如果我们只需要跟GQA相近的能力，那么是不是就可以再次减少KV Cache了？换言之，$d_c$没必要取$g(dk+dv)$，而是取更小的值，从而进一步压缩KV Cache，这就是MLA的核心思想”。

4.2 RoPE的兼容

RoPE与绝对位置相关，通过绝对位置计算两个token之间的相对位置信息：

$\textbf{R}_m\textbf{R}_n^T=\textbf{R}_{m-n}$

MLA加上RoPE之后：

$\textbf{q}_i^{(s)}=x_iW_q^{(s)}\textbf{R}_i, \ \ \ \ \ \textbf{k}_i^{(s)}=\textbf{c}_i\textbf{W}_{Uk}^{(s)}\textbf{R}_i$ $\textbf{q}_t^{(s)}\textbf{k}_i^{(s)T}=(x_tW_q^{(s)}\textbf{R}_t)(\textbf{c}_i\textbf{W}_{Uk}^{(s)}\textbf{R}_i)^T=x_tW_q^{(s)}\textbf{R}_{t-i}{W}_{Uk}^{(s)T}\textbf{c}_i^T$

不能固定$\textbf{W}_q^{(s)}\cdot\textbf{W}_{Uk}^{(s)T}$值作为$Q$的投影矩阵。
《缓存与效果的极限拉扯：从MHA、MQA、GQA到MLA》一文中探讨的其他方法
后来解决办法为每个head的$\textbf{Q}$和$\textbf{K}$新增$d_r$个维度来添加RoPE的信息，其中$\textbf{K}$新增的信息由每个head共享

dot-product的scaling变成了$\sqrt{d_k+d_r}$ $RoPE(\textbf{x}_i\textbf{W}_{qR}^{(s)})=\textbf{x}_i\textbf{W}_{qR}^{(s)}\textbf{R}_i,\ \ \ \ \ \textbf{W}_{qR}^{(s)}\in \mathbb{R}^{d\times d_r}$ $RoPE(\textbf{x}_i\textbf{W}_{kR})=\textbf{x}_i\textbf{W}_{kR}\textbf{R}_i,\ \ \ \ \ \textbf{W}_{kR}\in \mathbb{R}^{d\times d_r}$ $\textbf{c}_i=\textbf{x}_i\textbf{W}_c\in\mathbb{R}^{1\times d_c}$ $\textbf{q}_i^{(s)}=[\textbf{x}_i\textbf{W}_q^{(s)}, \textbf{x}_i\textbf{W}_{qR}^{(s)}\textbf{R}_i]\in \mathbb{R}^{1\times [d_k+d_r]},\ \ \ \ \ \textbf{W}_q^{(s)}\in \mathbb{R}^{d\times d_r}$ $\textbf{k}_i^{(s)}=[\textbf{c}_i\textbf{W}_{Uk}^{(s)}, \textbf{x}_i\textbf{W}_{kR}\textbf{R}_i]\in \mathbb{R}^{1\times [d_k+d_r]},\ \ \ \ \ \textbf{W}_{Uk}^{(s)}\in \mathbb{R}^{d\times d_r}$ $\textbf{v}_i^{(s)}=\textbf{c}_i\textbf{W}_{Uv}^{(s)}\in \mathbb{R}^{1\times d_v},\ \ \ \ \ \textbf{W}_{Uv}^{(s)}\in \mathbb{R}^{d_c\times d_v}$ 👇可以看到保留了$Q$的固定投影$\textbf{W}_q^{(s)}\cdot\textbf{W}_{Uk}^{(s)T}$和相对位置信息$\textbf{R}_{t-i}$ $\textbf{q}_t^{(s)}\textbf{k}_i^{(s)T}=(\textbf{x}_t\textbf{W}_q^{(s)})(\textbf{c}_i\textbf{W}_{Uk}^{(s)})^T+(\textbf{x}_t\textbf{W}_{qR}^{(s)}\textbf{R}_t)(\textbf{x}_i\textbf{W}_{kR}\textbf{R}_i)^T$ $=\textbf{x}_t(\textbf{W}_q^{(s)}\cdot\textbf{W}_{Uk}^{(s)T})\textbf{c}_i^T+\textbf{x}_t\textbf{W}_{qR}^{(s)}(\textbf{R}_{t-i})\textbf{W}_{kR}^T\textbf{x}_i^T$

4.3 MLA最终版本

“in order to reduce the activation memory during training”，最后MLA在训练阶段对$Q$的输入$\textbf{x}_i$也做了低秩投影，即 $\textbf{c}_i'=\textbf{x}_i\textbf{W}_{Dq}\in \mathbb{R}^{1\times d_c'},\ \ \ \ \ \textbf{W}_{Dq}\in \mathbb{R}^{d\times d_c'}$$$$\textbf{q}_i^{(s)}=[\textbf{c}_i'\textbf{W}_{Uq}^{(s)}, \textbf{c}_i'\textbf{W}_{qR}^{(s)}\textbf{R}_i]\in \mathbb{R}^{1\times [d_k+d_r]},\ \ \ \ \ \textbf{W}_{Uq}^{(s)}\in \mathbb{R}^{d_c'\times d_k},\textbf{W}_{qR}^{(s)}\in \mathbb{R}^{d_c'\times d_k}$ 最终版本的训练阶段：

$\textbf{u}_t = \textbf{o}_t\textbf{W}_o,\ \ \ \ \ \textbf{W}_o\in \mathbb{R}^{d\times hd_k}$ $\textbf{o}_t=[\textbf{o}_t^{(1)}, \textbf{o}_t^{(2)}, ..., \textbf{o}_t^{(h)}] \in \mathbb{R}^{1\times d}$ $\textbf{o}_t^{(s)} = Attention(\textbf{q}_t^{(s)}, \textbf{k}_{i\leq t}^{(s)}, \textbf{v}_{i\leq t}^{(s)}) = \sum^t_{i=1}softmax(\dfrac{\textbf{q}_t^{(s)}\textbf{k}_i^{(s)T}}{\sqrt{d_k+d_r}})\textbf{v}_i^{(s)}$ $\textbf{c}_i=\textbf{x}_i\textbf{W}_c\in\mathbb{R}^{d_c},\ \ \ \ \ \textbf{W}_c\in\mathbb{R}^{d\times d_c}$ $\textbf{c}_i'=\textbf{x}_i\textbf{W}_{Dq}\in \mathbb{R}^{1\times d_c'},\ \ \ \ \ \textbf{W}_{Dq}\in \mathbb{R}^{d\times d_c'}$ $\textbf{q}_i^{(s)}=[\textbf{c}_i'\textbf{W}_{Uq}^{(s)}, \textbf{c}_i'\textbf{W}_{qR}^{(s)}\textbf{R}_i]\in \mathbb{R}^{1\times [d_k+d_r]},\ \ \ \ \ \textbf{W}_{Uq}^{(s)}\in \mathbb{R}^{d_c'\times d_k},\textbf{W}_{qR}^{(s)}\in \mathbb{R}^{d_c'\times d_k}$ $\textbf{k}_i^{(s)}=[\textbf{c}_i\textbf{W}_{Uk}^{(s)}, \textbf{x}_i\textbf{W}_{kR}\textbf{R}_i]\in \mathbb{R}^{1\times [d_k+d_r]},\ \ \ \ \ \textbf{W}_{Uk}^{(s)}\in \mathbb{R}^{d_c\times d_k}$ $\textbf{v}_i^{(s)}=\textbf{c}_i\textbf{W}_{Uv}^{(s)}\in \mathbb{R}^{1\times d_v},\ \ \ \ \ \textbf{W}_{Uv}^{(s)}\in \mathbb{R}^{d_c\times d_v}$ $\textbf{q}_t^{(s)}\textbf{k}_i^{(s)T}=(\textbf{c}'_t\textbf{W}_{Uq}^{(s)})(\textbf{c}_i\textbf{W}_{Uk}^{(s)})^T+(\textbf{c}_t\textbf{W}_{qR}^{(s)}\textbf{R}_t)(\textbf{x}_i\textbf{W}_{kR}\textbf{R}_i)^T$ $=\textbf{c}'_t(\textbf{W}_{Uq}^{(s)}\cdot\textbf{W}_{Uk}^{(s)T})\textbf{c}_i^T+\textbf{c}'_t\textbf{W}_{qR}^{(s)}(\textbf{R}_{t-i})\textbf{W}_{kR}^T\textbf{x}_i^T$

最终版本的推理阶段：
$\textbf{u}_t = [\textbf{o}_t^{(1)}\textbf{W}_o^{'(1)},\textbf{o}_t^{(2)}\textbf{W}_o^{'(2)},...,\textbf{o}_t^{(h)}\textbf{W}_o^{'(h)}]$

$\textbf{W}'_o=[\textbf{W}_o^{'(1)},\textbf{W}_o^{'(2)},...,\textbf{W}_o^{'(h)}],\ \ \ \ \ \textbf{W}'_o\in \mathbb{R}^{d\times hd_k}$

$\textbf{W}’_o$融合了$\textbf{W}_o$和$\textbf{W}_v^{(g)}$得到的，在推理阶段是固定值 $\textbf{o}_t^{(s)} = Attention(\textbf{q}_t^{(s)}, \textbf{k}_{i\leq t}, \textbf{v}_{i\leq t}) = \sum^t_{i=1}softmax(\dfrac{\textbf{q}_t\textbf{k}_i^T}{\sqrt{d_k+d_r}})\textbf{v}_i,\ \ \ \ \ \textbf{v}_i=\textbf{c}_i\in \mathbb{R}^{1\times d_c}$ $\textbf{c}_i=\textbf{x}_i\textbf{W}_c\in\mathbb{R}^{d_c},\ \ \ \ \ \textbf{W}_c\in\mathbb{R}^{d\times d_c}$ $\textbf{c}_i'=\textbf{x}_i\textbf{W}_{Dq}\in \mathbb{R}^{1\times d_c'},\ \ \ \ \ \textbf{W}_{Dq}\in \mathbb{R}^{d\times d_c'}$ $\textbf{q}_i^{(s)}=[\textbf{c}_i'\textbf{W}_{Uq}^{(s)}\textbf{W}_{Uk}^{(s)T}, \textbf{c}_i'\textbf{W}_{qR}^{(s)}\textbf{R}_i]\in \mathbb{R}^{1\times [d_c+d_r]},\ \ \ \ \ \textbf{W}_{Uq}^{(s)}\in \mathbb{R}^{d_c'\times d_k},\textbf{W}_{qR}^{(s)}\in \mathbb{R}^{d_c'\times d_k},\textbf{W}_{Uk}^{(s)}\in \mathbb{R}^{d_c\times d_k}$
$\textbf{W}_{Uq}^{(s)}\cdot\textbf{W}_{Uk}^{(s)T}$作为$Q$的投影矩阵 $\textbf{k}_i=[\textbf{c}_i, \textbf{x}_i\textbf{W}_{kR}\textbf{R}_i]\in \mathbb{R}^{1\times [d_c+d_r]}$
$\textbf{k}$在存储时不需要考虑不同head

对于单个token：

MLA推理时需要的缓存：
- $\textbf{v}_i=\textbf{c}_i\in \mathbb{R}^{1\times d_c}$
- $\textbf{k}_=[\textbf{c}_i, \textbf{x}_i\textbf{W}_{kR}\textbf{R}_i]\in \mathbb{R}^{1\times [d_c+d_r]}$，$d_c+d_r=512+64=576$
MHA版本的缓存：$2\times d_k\times h=2\times 128\times128=32768$

👇图思想来源DeepSeek-v2 MLA 原理讲解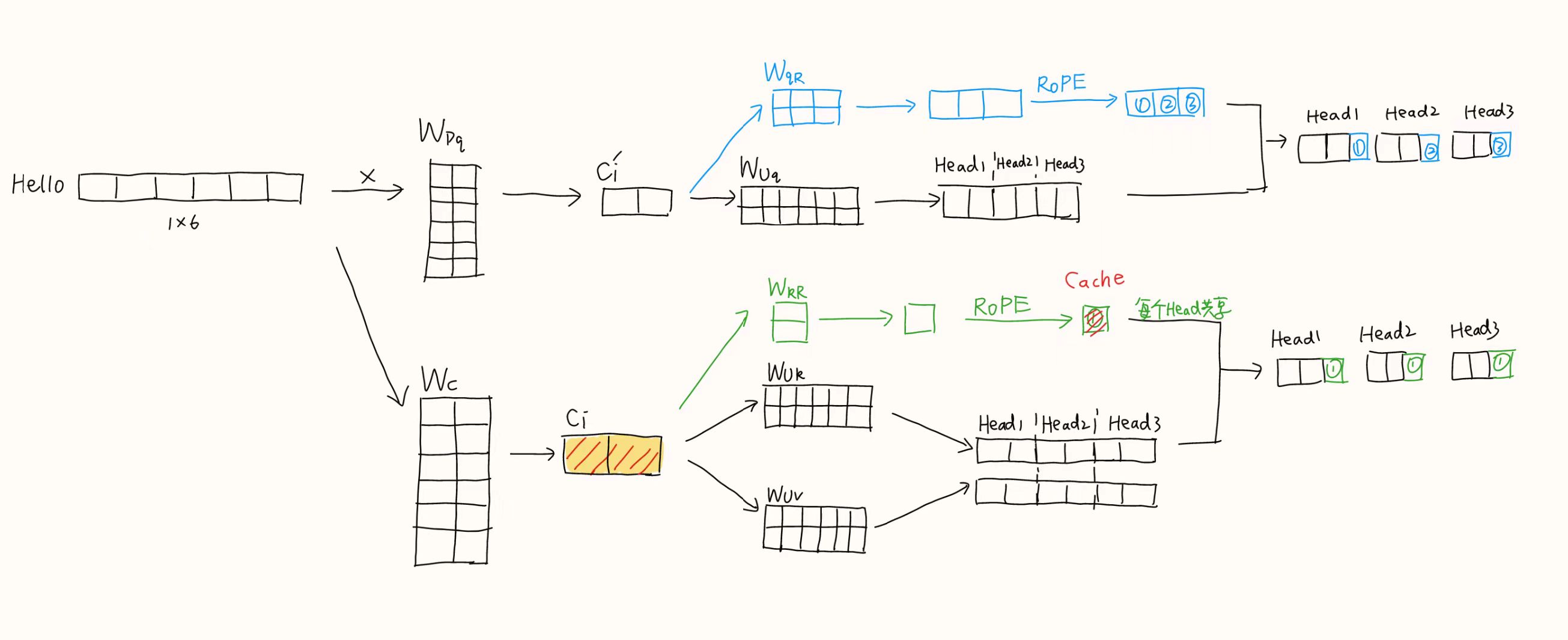 MLA投影过程(粗略)
《缓存与效果的极限拉扯：从MHA、MQA、GQA到MLA》一文中对MLA计算量增加和效率的讨论