第二章 CUDA中的线程组织
cudaDeviceSynchronize();:同步主机和设备,(因为调用输出函数时,输出流先放在缓冲区,但是缓冲区不会自动刷新,只有遇到某种同步操作时才会刷新),如果没有这句话是不会执行核函数的内容
dim3和unit3的区别
unit3:是一个结构体,具有x、y、z三个成员。适用blockIdx和threadIdxdim3:是一个结构体,和unit3类似,适用blockDim和gridDim- 二者关系,xxxIdx.a的取值范围是yyyDim.a-1,如:
blockIdx.x的取值范围是gridDim.x-1
第三章 简单CUDA程序的基本框架
3.2.2 设备内存的释放与分配
cudaMalloc()
cudaError_t cudaMalloc(void **address, size_t size);address:待分配设备内存的指针。因为内存(地址)本身就是一个指针,所以address是指针的指针size:待分配内存的字节数cudaError_t:作为返回值,如果调用成功则返回cudaSuccess(void **):将某一种类型的双重指针变为void类型的双重指针- 功能是改变指针d_x本身的值,即将一个指针赋值给d_x,因此要取d_x的地址,即
&d_x,同时该函数不是返回一个指针 - 配合
cudaFree()函数使用
3.2.3 主机与设备之间数据的传递
cudaError_t cudaMemcpy
(
void *dst, // 目标地址
const void *src, // 源地址
size_t count, // 复制数据的字节数
enum cudaMemcpyKind kind // 标志数据传递方向
);cudaMemcpy + Host/Device + To + Device/Host
或者cudaMemcpyDefault
3.2.4 核函数中数据与线程的对应
void __global__ add(const double *x, const double *y, double*z)
{
const int n = blockDim.x * blockIdx.x + threadIdx.x;
z[n] = x[n] + y[n];
}主机中的add函数需要循环,设备中的不需要,只需要数组元素指标与线程指标一一对应即可,在3.3add1.cu中就用了const int n = blockDim.x * blockIdx.x + blockIdx.x来实现对应关系(而主机中的需要用for(int n=0; n<N; n++))
3.2.6 核函数中if语句的必要性
N为数组元素,$grid_size=\dfrac{N}{block_size}$,如果有余数需要+1,此时线程数为N+block_size,因为grid_size每加一,就多一个block,每一个block有block_size个线程,所以此时线程数为N+block_size
| 原本 | 后来 | |
|---|---|---|
| N | $10^8$ | $10^8+1$ |
| block_size | 128 | 128 |
| grid_size | $\dfrac{10^8}{128}=781250$ | $\dfrac{10^8}{128}+1=781251$ |
| 实际的线程数$n=block_size*grid_size$ | $10^8$ | $10^8+128$ |
因此需要加上if(n>=N) return;,如果不加上这句,会出现非法的设备内存操作
第四章 CUDA程序的错误检验
- 在定义宏时,如果一行写不下,则需要在末尾写”\\\”,表示续行
- 用自定义的宏函数
CHECK检查运行时API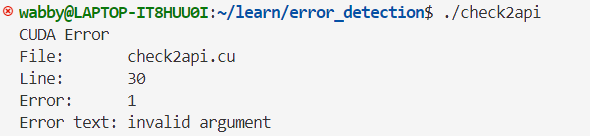
- 用以下两句检查核函数
只要在核函数的调用之后 还有其他任何能返回错误值的API函数进行同步调用,都能触发主机与设备的同步并捕捉到核函数调用中可能发生的错误。CHECK(cudaGetLastError()); // 捕捉第二个语句之前的最后一个错误 CHECK(cudaDeviceSynchronize()); // 捕捉是否有无法同步主机与设备的错误。因为核函数的调用是异步的,即主机发出调用核函数的命令后会执行后面的语句,不会等待核函数
一般情况下,如果需要获得准确的出错位置,需要显式同步。例如调用cudaDeviceSynchronize()函数,或者设置
$ export CUDA_LAUNCH_BLOCKING=1设置完毕后,所有核函数的调用都是同步的,但是最好只用于调试程序,因为这样会影响程序的性能。
❓这个cuda-memcheck没给我check出来错误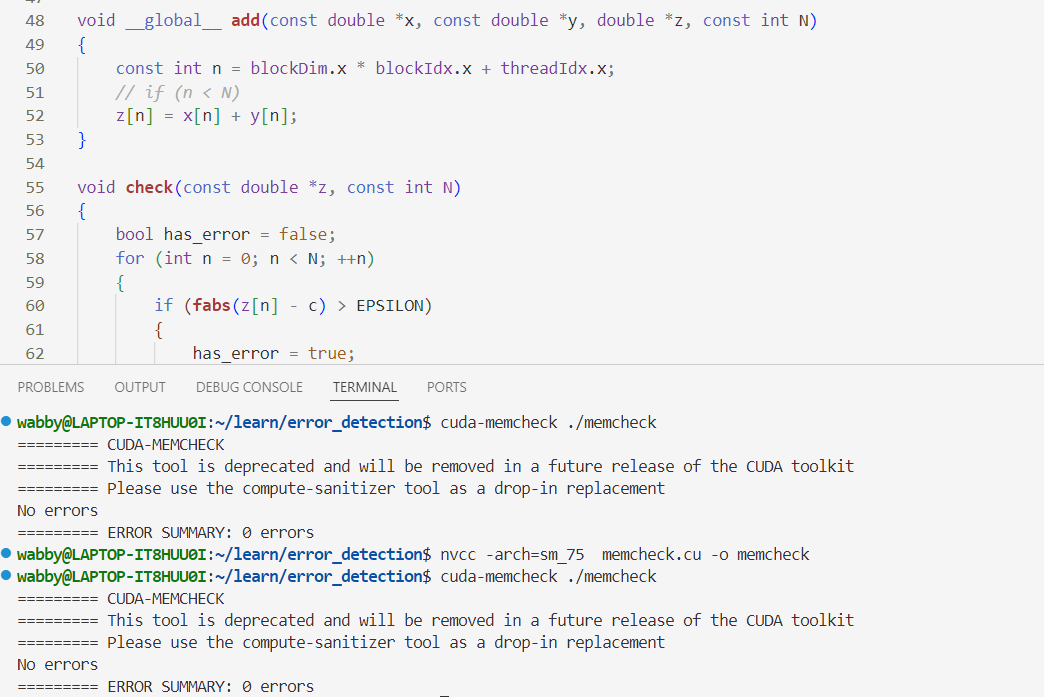
第五章 获得GPU加速的关键
5.1.1 为C++程序计时
选择浮点数精度
- 单精度浮点数的运行时间👇
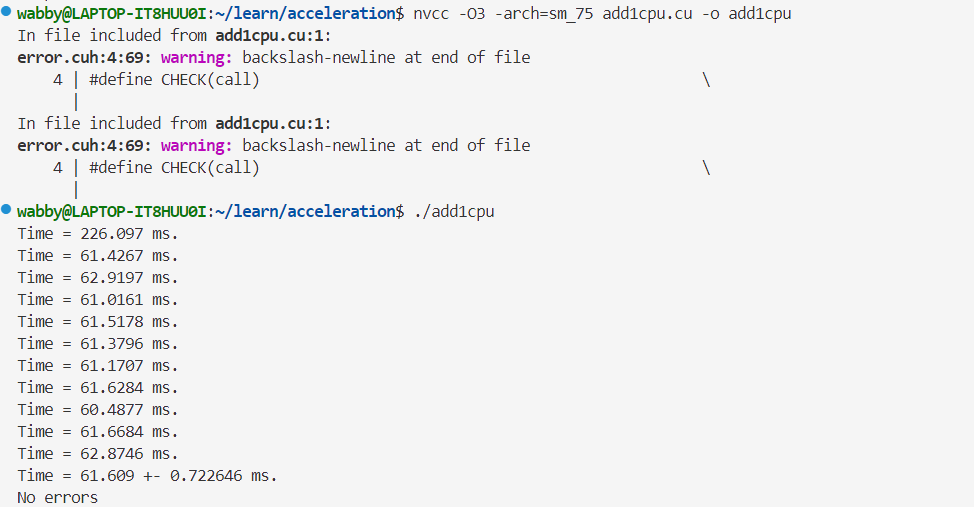
- 双精度浮点数的运行时间👇
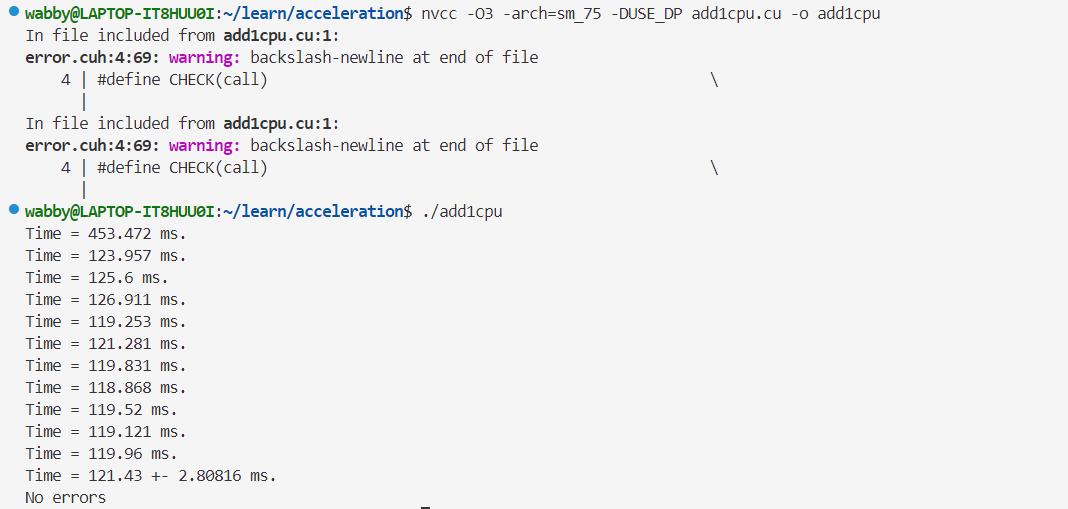
5.1.2 为CUDA程序计时
- 仅核函数
- 单精度👇
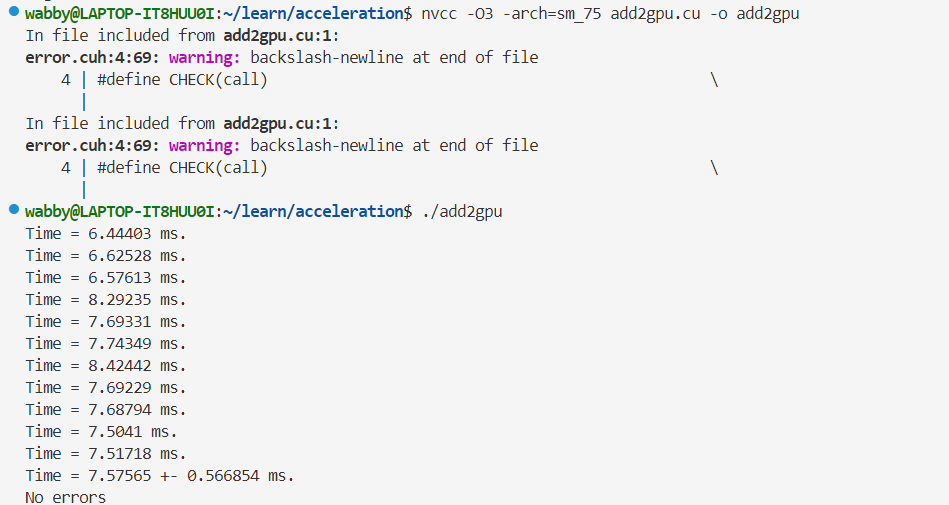
- 双精度👇
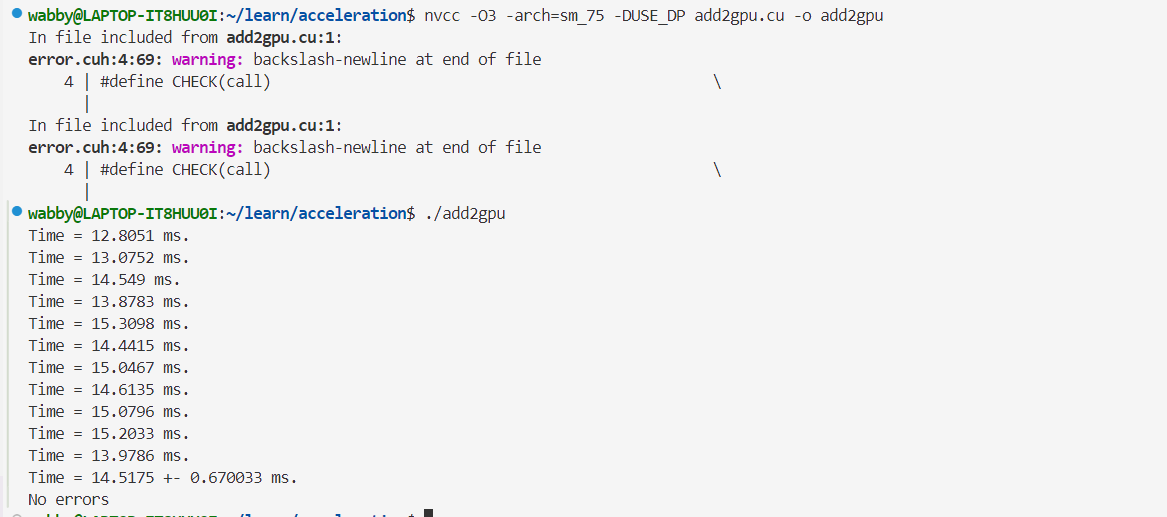
- 核函数与数据复制
- 单精度👇
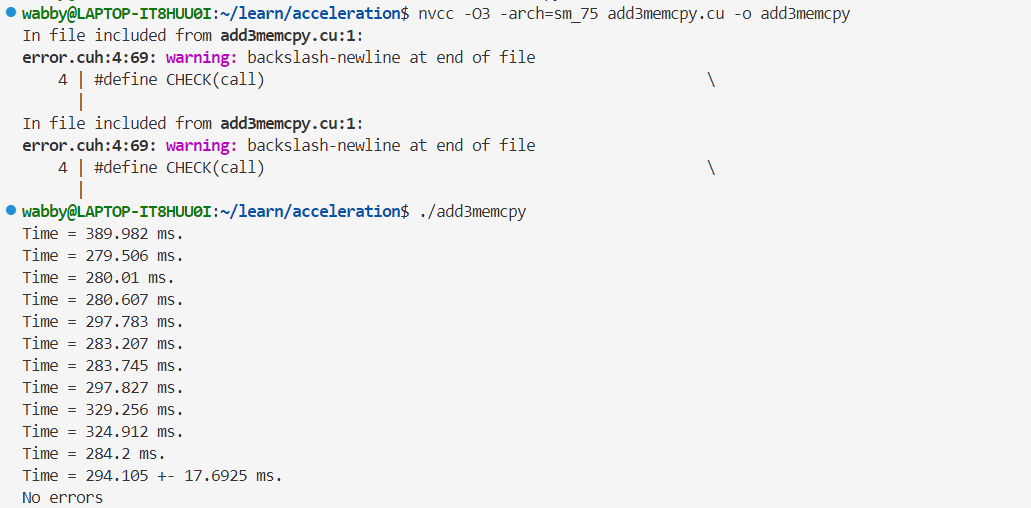
- 双精度👇
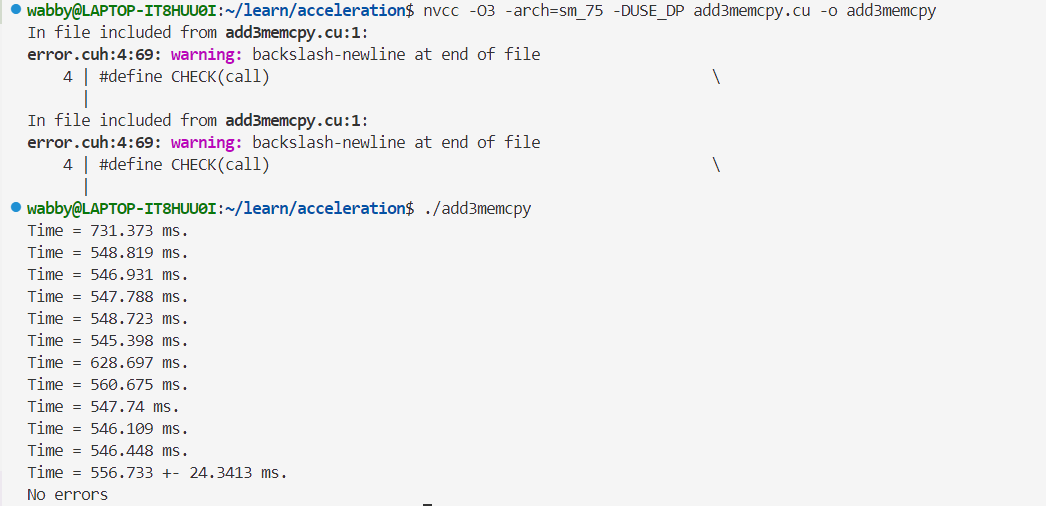
对比是否加入了数据复制的用时,可以发现: - 核函数的运行时间比数据复制时间要短的多,约占2.5%
- 如果一个程序的任务仅仅将来自主机端的两个数组相加,再将结果传到主机端,使用GPU的话效率更加低下,(CUDA程序相较于C++程序性能降低
关于nvprof
是一个可用于对CUDA程序进行更多性能剖析的CUDA工具箱里的可执行文件,如果设备计算能力大于8.0不可用,输入nsys nvprof可用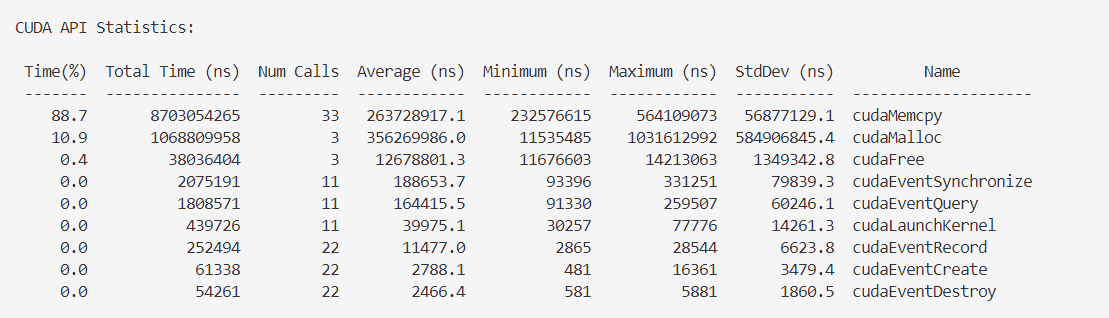
- 第一列是每类操作(第七列Name)占用时间百分比
- 第二列时每类操作所用的时间
- 第三列是每类操作被调用的次数
- 第四列是每类操作单词调用所用时间的平均值
- 第五列和第六列分别是每类操作单次调用所用时间的最小值和最大值
5.2.1 数据传输的比例
避免过多的数据经由(连接GPU和CPU)PCIe传递,必须尽量缩减数据传输所花时间的比例(数据在GPU和CPU上传输的时间比计算本身要多的话就得不偿失了)。理论上GPU的显存带宽为几百兆字节,常用的PCIe仅有16GB/s的带宽。
nvcc -O3中的-O3是告诉编译器尽可能多地进行优化
5.2.2 算数强度
进行较复杂的浮点运算,可能会得到更高的加速比,于是将之前的数组相加函数进行更改为👇
void arithmetic(real *x, const real x0, const int N)
{
for(int n=0; n<N; ++n)
{
real x_tmp = x[n];
while(sqrt(x_tmp) < x0)
{
++x_tmp;
}
x[n] = x_tmp;
}
}- CPU
- 单精度👇
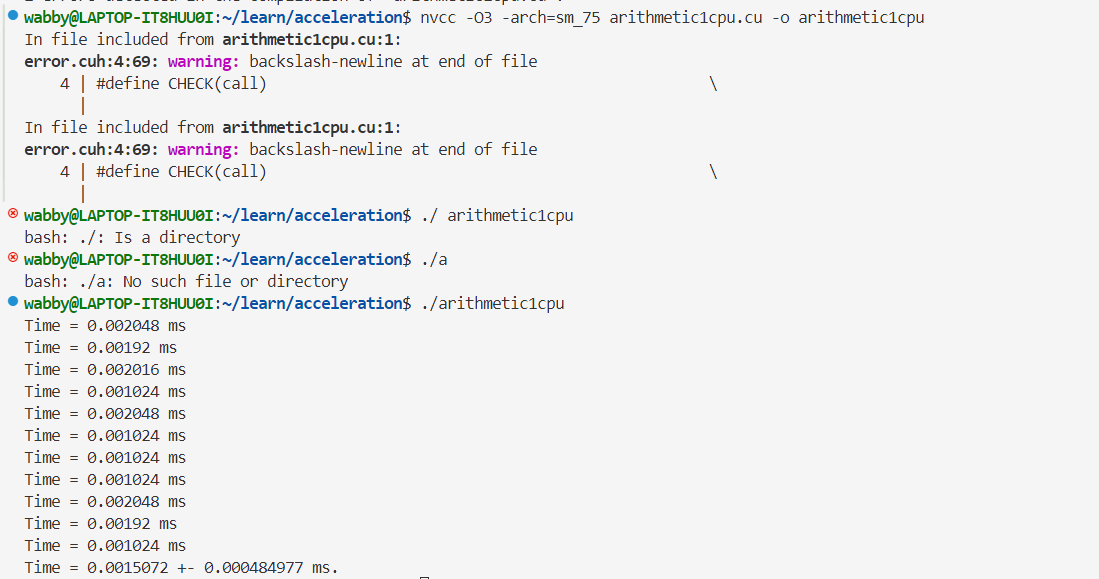
- 双精度👇
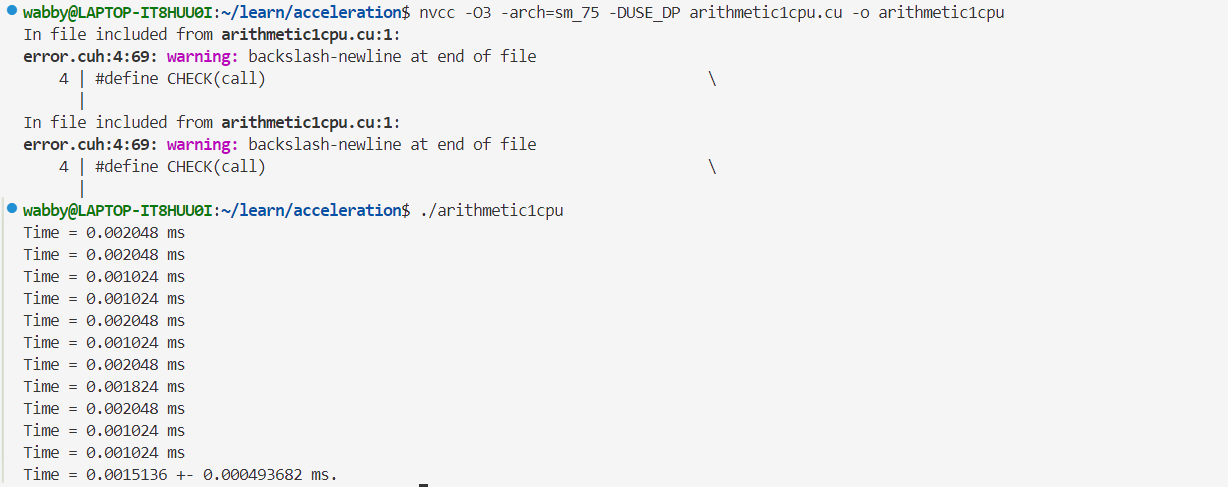
- GPU
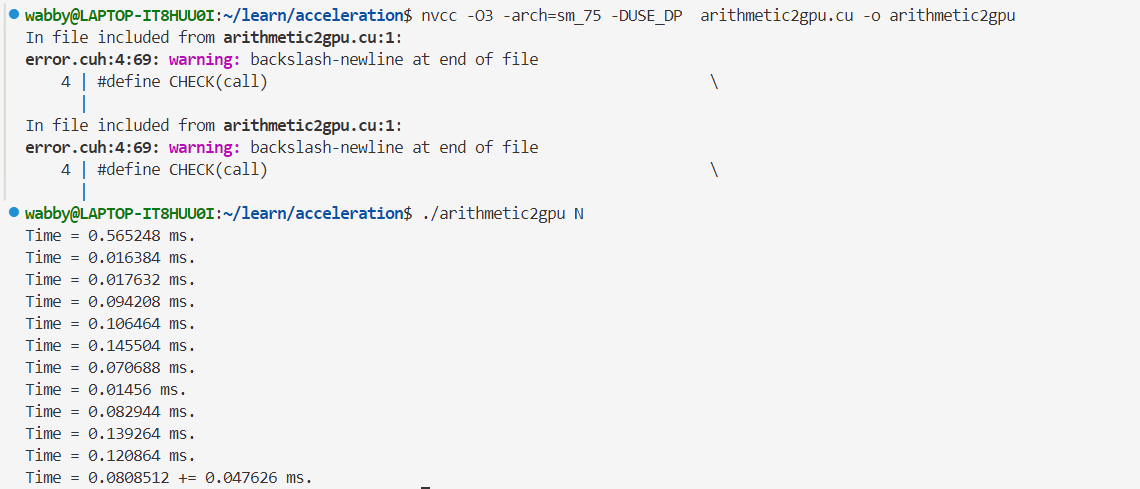
原本执行程序是.\arithmetic2gpu,因为有const int N = atoi(argv[1]);,所以变成.\arithmetic2gpu N,N可以是任何数字,在命令行中手动输入,将会被读取到程序中的N
- 单精度👇
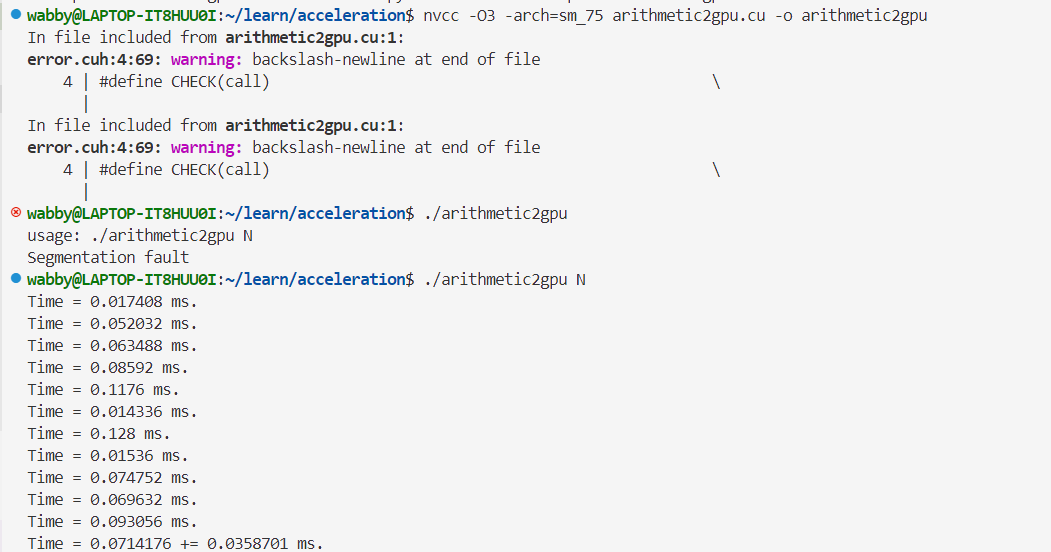
双精度👇
5.2.3 并行规模
并行规模可用GPU中总的线程数目来衡量
小结:数据传输比例小——减少主机与设备之间的数据传输
- 核函数的算术强度较高——提高核函数的算术强度
- 核函数中定义的线程数目较多——增大核函数的并行规模
第六章 CPU的组织内存
6.2.1 全局内存
在核函数中,可直接对静态全局内存变量进行访问,并不需要将它们以参数的形式传给核函数,即:
直接访问静态全局内村变量(d_x和d_y[])👇__device__ int d_x = 1; __device__ int d_y[2]; __global__ void my_kernel(void) { d_y[0] += d_x; // 直接访问 d_y[1] += d_x; // 直接访问 printf("d_x = %d\t d_y[0] = %d\t d_y[1] = %d\n", d_x, d_y[0], d_y[1]); } int main(int argc, char *argv[]) { ... my_kernel<<<1,1>>>(); // 无需传参 ... }(d_data和value)作为参数传给核函数
__global__ void myKernel(int *data, int value) { int idx = threadIdx.x; data[idx] = value; } int main() { int *d_data; int value = 10; cudaMalloc(&d_data, sizeof(int) * N); myKernel<<<1, N>>>(d_data, value); // 需要传参(d_data和value) cudaFree(d_data); return 0; }不可在主机函数中直接访问静态全局内存变量,但可以用
cudaMemcpyToSymbol()和cudaMemcpyFromSymbol()函数在静态全局内存与主机内存之间传输数据,这两个CUDA运行时API函数如下(symbol指的是静态全局内存变量)cudaError_t cudaMemcpyToSymbol ( const void* symbol, // 静态全局内存变量名 const void* src, // 主机内存缓冲区指针 size_t count, // 复制的字节数 size_t offset = 0, // 从symbol对应设备地址开始偏移的字节数 cudaMemcpyKind kind = cudaMemcpyHostToDevice // 可选参数 ); cudaError_t cudaMemcpyFromSymbol ( void *dst, // 主机内存缓冲区指针 const void* symbol, // 静态全局内存变量 size_t count, // 复制的字节数 size_t offset = 0, // 从symbol对应设备地址开始偏移的字节数 cudaMemcpyKind kind = cudaMemcpyDeviceToHost // 可选参数 )- 特点
- 所有线程都能访问,全局内存对整个网格的所有线程可见
- 没有放在GPU芯片上,具有较高延迟和较低的访问速度;是所有设备中内存最大的,容量基本上就是显存容量
- 可读可写
- 生命周期:从主机端用
cudaMalloc()对他们分配开始,到主机端用cudaFree()释放他们的内存结束
6.2.2 常量内存
- 是有常量缓存的全局内存,仅有64KB
- 可读不可写
- (因为有缓存)访问速度比全局内存高,速度高的前提是一个线程束中的线程(一个线程块中相邻的32个线程)要读取相同的常量内存数据
- 使用例子:用
__constant__定义变量、const int N(这是在主机端定义的变量,通过传值的方式传送给核函数中的线程使用),核函数对常量内存的访问比对全局内存的访问要快 - 给核函数传递的参数存放在常量内存中,最多只能用4KB常量内存
6.2.4 寄存器
核函数中定义的且存放在寄存器的有:
- 不加任何限定符的变量
- 不加任何限定符的数组(也有可能在局部内存中)
- 内建变量(如
gridDim、blockDim、blockIdx、threadIdx、warpSize等等)
寄存器可读可写: - 写入:
const int n = blockDim.x * blockIdx.x + threadIdx.x中的n就是一个寄存器变量 - 读出:
z[n] = x[n] + y[n]
寄存器变量仅被一个线程可见(以可读可写处代码为例): - 每个线程都有一个变量
n的副本,虽然都是同一个变量名n,但是不同线程中该寄存器变量的值可以不同。而且每个线程只能对它的副本进行读写 - 这就是为什么在主机函数中需要用到
for循环写入和读出n(for int n=0; n<N; N++和z[n]=x[n]+y[n]),而核函数只需要const int n = blockDim.x * blockIdx. + threadIdx.x即可定位到不同的n,因为都是副本
6.2.5 局部内存
寄存器中放不下的变量、索引值不能在编译时就确定的数组都有可能放在局部内存中
6.2.6 共享内存
- 和寄存器类似,速度仅次于寄存器的读写速度
- 共享内存对整个线程块可见,每个线程块拥有一个共享内存变量的副本,共享内存变量的值在不同的线程块中可以不同。一个线程块中的所有线程都可以访问该线程块的共享变量副本,但是不能访问其他线程块的共享内存变量副本
- 主要作用是减少对全局内存的访问
6.4 用CUDA运行时API函数查询设备
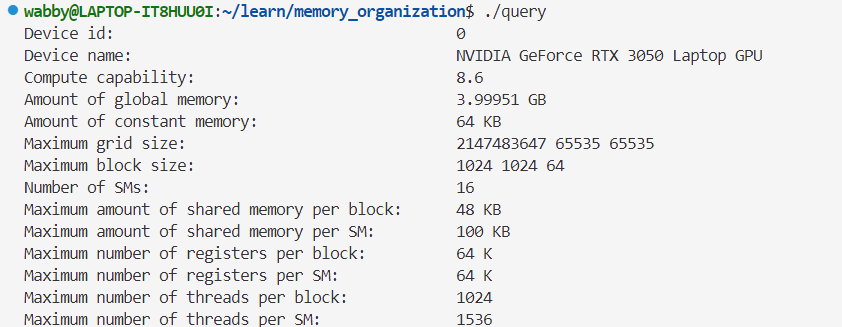
第七章 全局内存的合理使用
7.1 全局内存的合并与非合并访问
$合并度=\dfrac{线程束请求的字节数}{由该请求导致的所有数据传输处理的字节数}$
数据传输对数据地址的要求:在一次数据传输中,从全局内存转移到L2缓存的一片内存首地址一定是一个最小颗粒度(本例是32)的整数倍。
- 顺序的合并访问
__global__ void add(float *x, float *y, float *z) { int n = threadIdx.x + blockIdx.x * blcokDim.x; z[n] = x[n] + y[n]; }
- 第一个线程块(blockIdx.x=0)中的线程束将访问数组
x中第0~31个元素(每个元素类型为float,占四个字节),则对应32×4=128字节的连续内存 - 首地址一定是256字节的整数倍(使用CUDA运行时API如
cudaMalloc分配的内存的首地址至少是256字节的整数倍) - 这样只需要访问4次数据传输即可完成(要求:一次数据传输只能从全局内存读取地址为0~31字节、32~63字节等片段的数据。如果线程束请求的全局内存数据的地址刚好为0~127字节或者128~256字节,就能与4次数据传输(0~31、32~63、64~95、96~127四次)所处理的数据完全吻合)
- 合并度为100%
- 乱序的合并访问
__global__ void add_permuted(float *x, float *y, float *z) { int tid_permuted = threadIdx.x ^ 0x1; int n = tid_permuted + blockIdx.x * blcokDim.x; z[n] = x[n] + y[n]; }
threadIdx.x ^ 0x1异或,将threadIdx.x最后一位翻转- 仅把线程块中奇偶次序调转。如第一个线程块中,原本n的顺序为0、1、2、3…。变为1、0、3、2…,即只不过线程号与数组元素指标不完全一致
- 合并度为100%
- 不对齐的非合并访问
void __global__ add_offset(float *x, float *y, float *z) { int n = threadIdx.x + blockIdx.x * blcokDim.x + 1; z[n] = x[n] + y[n]; } add_permuted<<<128, 32>>>(x, y, z);
- 以第一个线程块为例,第一个线程块中的线程束将访问数组x中第1~32个元素。
- 假如数组x的首地址为256,那么
x[0]为256~259,x[1]为260~263,x[32]为382~387 - 这将触发5次数据传输,对应的内存地址为256~287字节、288~319字节、320~351字节、352~383字节和384~415字节
- 合并度为$\dfrac{4}{5}×100=80\%$
- 跨越式的非合并访问
void __global__ add_stride(float* x, float* y, float* z) { int n = blockIdx.x + threadIdx.x * gridDim.x; z[n] = x[n] + y[n]; } add_stride<<<128, 32>>>(x, y, z);
- 第一个线程块中的线程束将访问数组x中指标为
0 + threadIdx.x * gridDim.x=1*128、2*128、3*128...的元素 - 每一对数据都不在一个连续的32字节的内存片段,因此该线程束的访问将触发32次数据传输
- 合并度为$\dfrac{4}{32}×100\%=12.5\%$
- 广播式的非合并访问
void __global__ add_broadcast(float* x, float* y, float* z) { int n = blockIdx.x + threadIdx.x * gridDim.x; z[n] = x[0] + y[n]; } add_stride<<<128, 32>>>(x, y, z);
- 第一个线程块中的线程束将一致地访问数组x中的第0个元素。这实际上只需要一次数据传输(处理32字节的数据),但整个线程束都在访问同一个内存地址
x[0],只使用了4字节的数据 - 合并度为$\dfrac{4}{32}×100\%=12.5\%$
7.2 例子:矩阵转置
transpose1():对矩阵A中数据的访问(读取)是顺序的(/合并的),对矩阵B中数据的访问(写入)不是顺序的(/非合并的)if(nx < N && ny < N) { B[nx * N + ny] = A[ny * N + nx]; }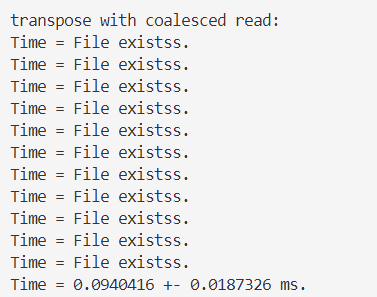
transpose2():对矩阵A中数据的访问(读取)不是顺序的(/非合并的),对矩阵B中数据的访问(写入)是顺序的(/合并的)
if(nx < N && ny < N)
{
B[ny * N + nx] = A[nx * N + ny];
}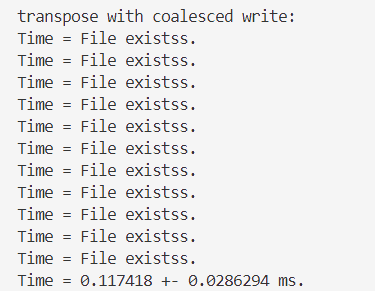
可以发现transpose2()的用时比transpose1()的更久?
书上原话:
- 在不能满足读取和写入都是合并的情况下,一般来说应当尽量做到合并地写入
- 书上的结果是2比1用时更短,因为编译器能够判断一个全局内存变量在整个核函数的范围都只可读,则会自动用函数
__ldg()读取全局内存,从而对数据的读取进行缓存,缓解非合并访问带来的影响。而对于全局内存的写入则没有类似的函数可用
👇用了别人的代码后
第八章 共享内存的合理使用
8.1 例子:数组归约计算
- C++实现计算长度较大的累加计算时,会出现”大数吃小数“的现象
- CUDA实现比C++实现上述内容时要稳健得多
单精度👇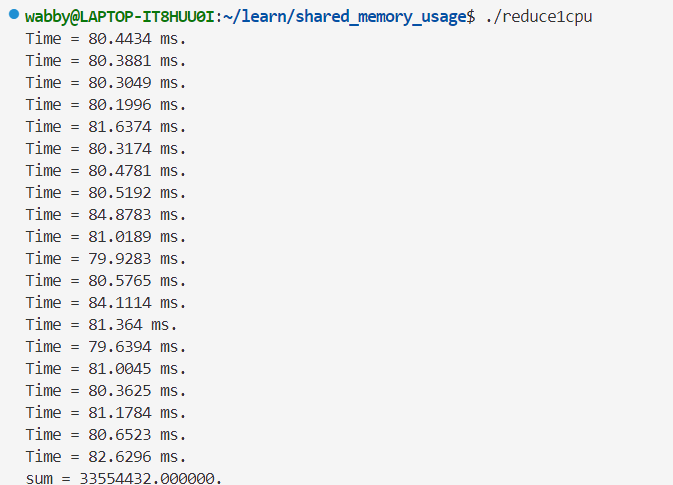
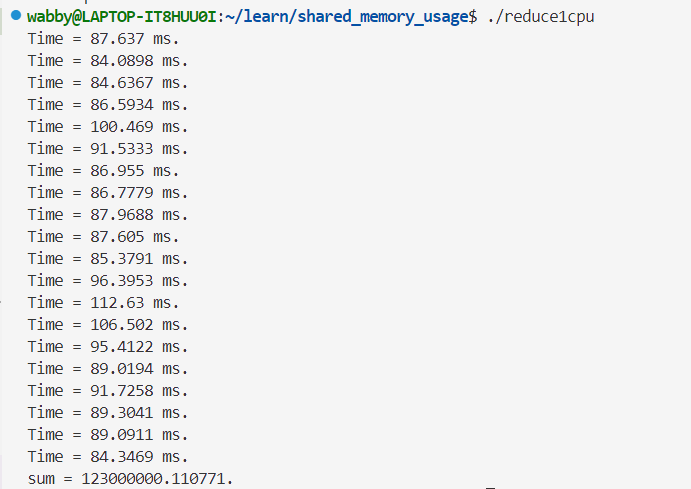
上面两个出现大数吃小数的情况
| 精度 | reduce_global | reduce_shared | reduce_dynamic | 结果 |
|---|---|---|---|---|
| float | 6~7ms | 7~8ms | 7~9ms | 123633392.000000. |
| double | 9~11ms | 15~17ms | 15~18ms | 122999999.998770. |
单精度的结果没有那么离谱,但是离正确答案还有一段距离
8.1.1 仅使用全局内存
- 访问频繁
- 使用折半归约法
- 假设核函数的网格大小和线程块大小的乘积为
N - 对于多线程的程序,两个不同线程中指令的执行次序可能和代码中展现的次序不同
- 例(循环的前两次):
// 循环的第一次 if(n < N/2){d_x[n] += d_x[n + N/2];} // 在这次操作中可能会有向数组d_x[N/4]写入数据的操作; // 循环的第二次 if(n < N/4){d_x[n] += d_x[n + N/4];} // 有可能在线程n=0开始执行这句时,n=N/4还没执行完上一行 [1 2 3 4 5 6 7 8] N = 8, N/2 = 4, 第一次n=0~3, d_x[0] += d[4] 等价于 d_x[0]= 1+5 = 6 [6 8 10 12] N/4 = 2, 第二次n=0~1, 可能会出现上面还没加完,就执行这里的情况 - 解决方法:要保证核函数中语句的执行顺序与出现顺序一致,用同步函数
__syncthreads()- 只针对一个线程块中的线程(即只能够同步单个线程块中的线程)
void __global__ reduce_global(real* d_x, real* d_y) { const int tid = threadIdx.x; real* x = d_x + blockDim.x * blockIdx.x; // 不同的线程块指向全局内存中的不同地址 // 上面也可以写成 real* x = &d_x[blockDim.x * blockIdx.x]; // d_x是动态数组,数组名就是数组首地址 // 取d_x[blockDim.x + blockIdx.x]的地址等价于首地址+偏移量(bDimx.x+bIdx.x) // 定义的x在不同的线程块中指向全局内存中的不同地址! for(int offset = blockDim.x >> 1; offset > 0; offset >>= 1) { if(tid < offset) { x[tid] += x[tid+offset]; } __syncthreads(); // 保证同一个线程块内地线程按照代码出现地顺序执行命令 } // 上述for循环保证各个线程块内对其中的数据独立地进行归约 if(tid == 0) { d_y[blockIdx.x] = x[0]; } }
- 只针对一个线程块中的线程(即只能够同步单个线程块中的线程)
real* x = d_x + blockDim.x * blockIdx.x;- ==x在不同的线程块中指向全局内存中的不同地址==,可以理解为上面每一个小数组(书上的例子的小数组长度为$10^8$)为一个
d_x,不同的线程块对d_x中不同的部分进行归约,(同一个线程块中的线程的处理速度不一致? - 该核函数仅将一个长度为$10^8$的数组
d_x归约到一个长度为$\dfrac{10^8}{128}$的数组d_y(书上的操作是把d_y从设备复制到主机里并在主机继续对d_y进行归约得到最终的结果,实际上这样不是很高效) - 利用位操作,将
blockDim.x/2和offset/=2分别写成了blockDim.x>>1和offset>>=1,在核函数中,位操作比对应的整数操作高效。当所涉及的变量在编译期间就知道其可能的取值,编译器会自动用伪操作取代相应的整数操作
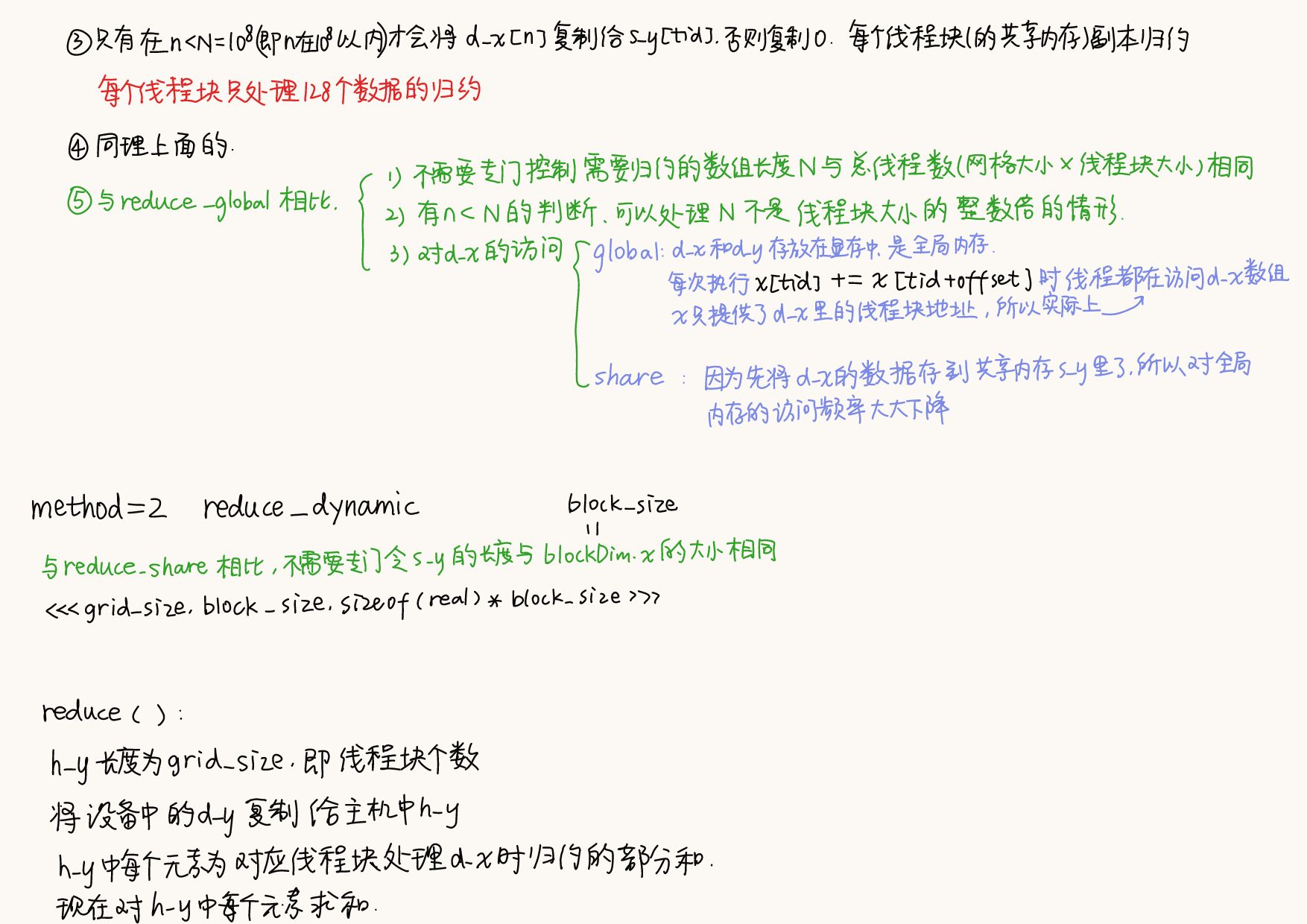
8.1.2 使用共享内存
共享内存的主要作用:①减少核函数中对全局内存的访问次数②提高全局访问的合并度
共享内存的特点:对整个线程块可见,每个线程块都有一个共享内存变量的副本
定义共享内存变量__shared__
- 在一个核函数中定义一个共享内存变量,就相当于在每个线程块中有一个该变量的副本,虽然每个副本共用一个变量名,但是每个副本都不一样
- 核函数中,对共享内存变量的操作都是同时作用在所有的副本上的
__global__ void reduce_shared(real *d_x, real *d_y) { const int tid = threadIdx.x; const int bid = blockIdx.x; const int n = bid*blockDimx.x + tid; __shared__ real s_y[128]; // 共享内存的数组长度与核函数的执行配置参数blockDim.x一样,如果这里写错了,会引起错误或降低核函数性能 s_y[tid] = (n<N) ? d_x[n] : 0.0; // 将全局内存中的数据复制到共享内存中 __syncthreads(); for(int offset = blockDim.x >> 1; ) { if(tid < offset) { s_y[tid] += s_y[tid + offset]; } __syncthreads(); } if(tid==0) { d_y[tid] = s_y[0]; } }
- 一般来说,在核函数中对共享内存访问的次数越多,则由于使用共享内存带来的加速效果越明显
- 因为有
n<N的判断,该函数能够处理N不是线程块大小的整数倍的情形
8.1.3 使用动态共享内存
使用动态共享内存可以减少8.1.2中“共享内存的数组长度与核函数的执行配置参数需与blockDim.x一样,如果这里写错了,会引起错误或降低核函数性能”错误发生的概率
将静态内存改为动态内存的修改:
<<<grid_size, block_size, sizeof(real) * block_size>>>,第三个参数就是核函数中每个线程块需要定义的动态共享内存的字节数- 改变核函数中共享内存变量的声明方式
- 静态:
__shared__ real s_y[128]; - 动态:`extern shared real s_y[];
- 静态:
单精度👇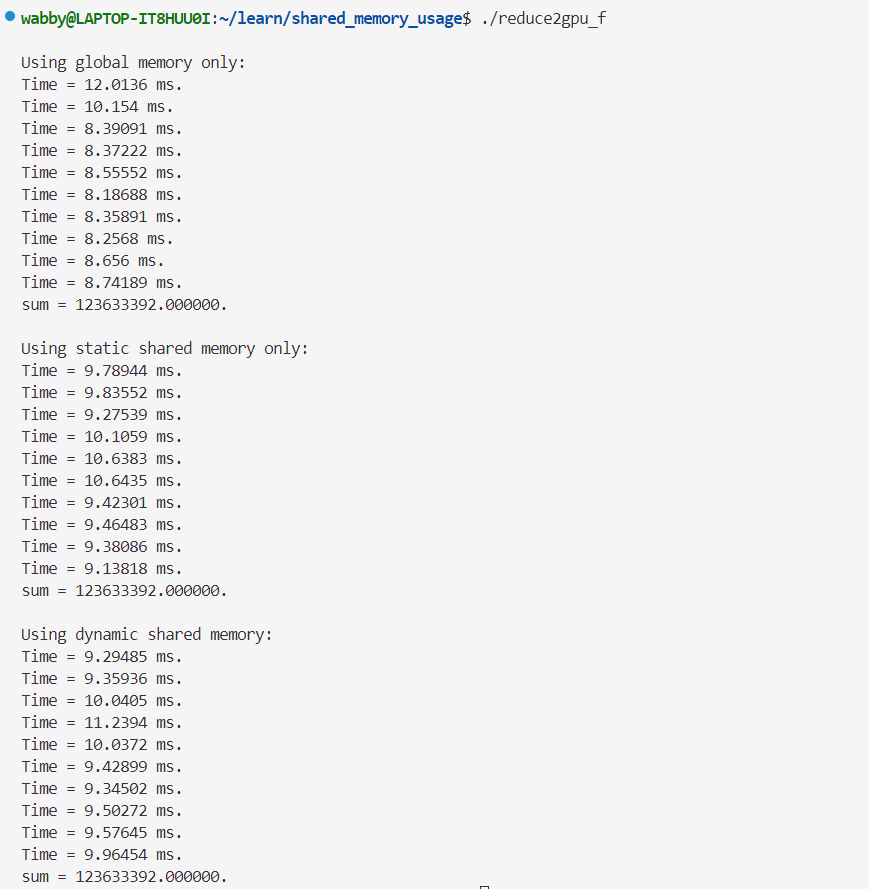
双精度👇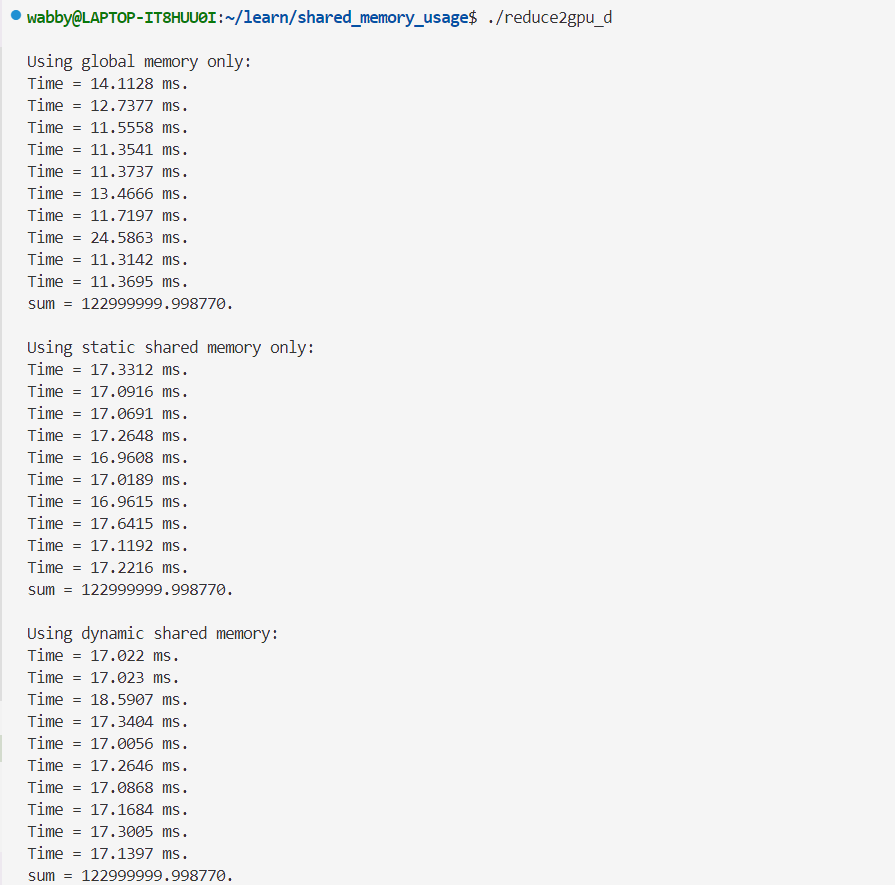
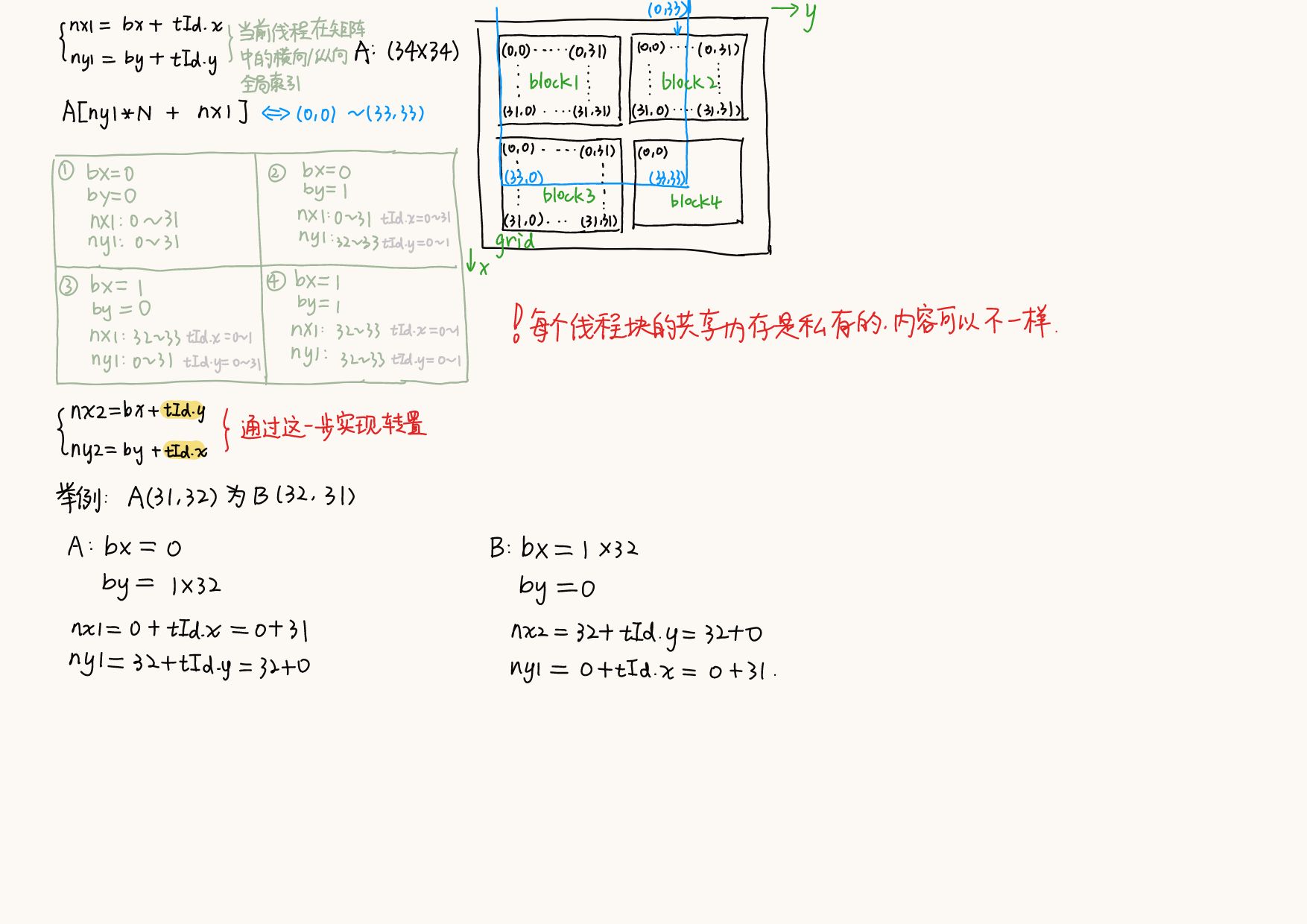
8.2 使用共享内存进行矩阵转置
利用共享内存可以改善全局内存的访问模式,使得对全局内存的读和写都是合并的
__gobal__ void transpose1(const real *A, real *B, const int N)
{
__shared__ real S[TILE_DIM][TILE_DIM]; // 用一个线程块处理一片32x32的矩阵
int bx = blockIdx.x * TILE_DIM;
int by = blockIdx.y * TILE_DIM;
int nx1 = bx + threadIdx.x;
int ny1 = by + threadIdx.y;
if(nx1 < N && ny1 < N)
{
S[threadIdx.y][threadIdx.x] = A[ny1 * N + nx1]; // 因为相邻的threadIdx.x与全局内存中相邻的数据对应,所以这里对全局内存的访问是合并的
}
__syncthreads();
int nx2 = bx + threadIdx.y;
int ny2 = by + threadIdx.x;
if(nx2 < N && ny2 < N)
{
B[nx2 * N + ny2] = S[threadIdx.x][threadIdx.y];
}
}上述代码的节选部分👇
int nx2 = bx + threadIdx.y;
int ny2 = by + threadIdx.x;
// 上面这两行改变了对全局内存的访问方式
// 这里的bx和by根据blockIdx.x和blockIdx.y的变化而变化。可以视为某个线程块在全局中的偏移量
if(nx2 < N && ny2 < N)
{
B[nx2 * N + ny2] = S[threadIdx.x][threadIdx.y]; // 相邻的threadIdx.x与全局内存中的数组B中的相邻的数据对应
//B的相邻是ny2,ny2又和threadIdx.x一致相邻
}第七章
transpose1()相关部分👇__global__ void transpose1(const real* A, real* B, const int N)
{
const int nx = blockIdx.x * blockDim.x + threadIdx.x;
const int ny = blockIdx.y * blockDim.y + threadIdx.y;
if(nx < N && ny < N)
{
B[nx * N + ny] = A[ny * N + nx];
}
}跟上面代码一样的写法👇
int nx2 = bx + threadIdx.x;
int ny2 = by + threadIdx.y;
// 这样子定义nx2和ny2的话和上面全局内存的访问方式一样
if(nx2 < N && ny2 < N)
{
B[nx2 * N + ny2] = S[threadIdx.y][threadIdx.x];
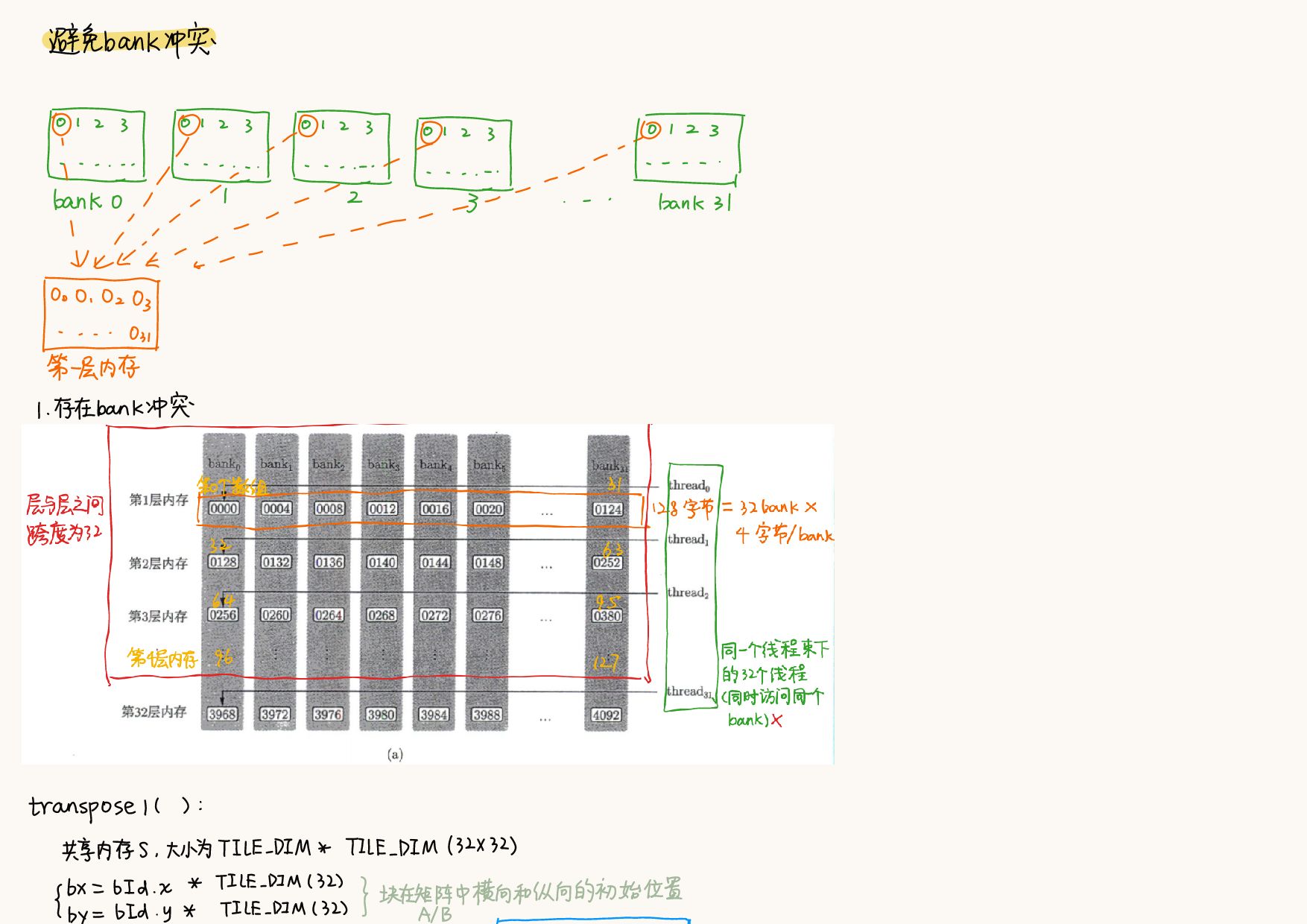
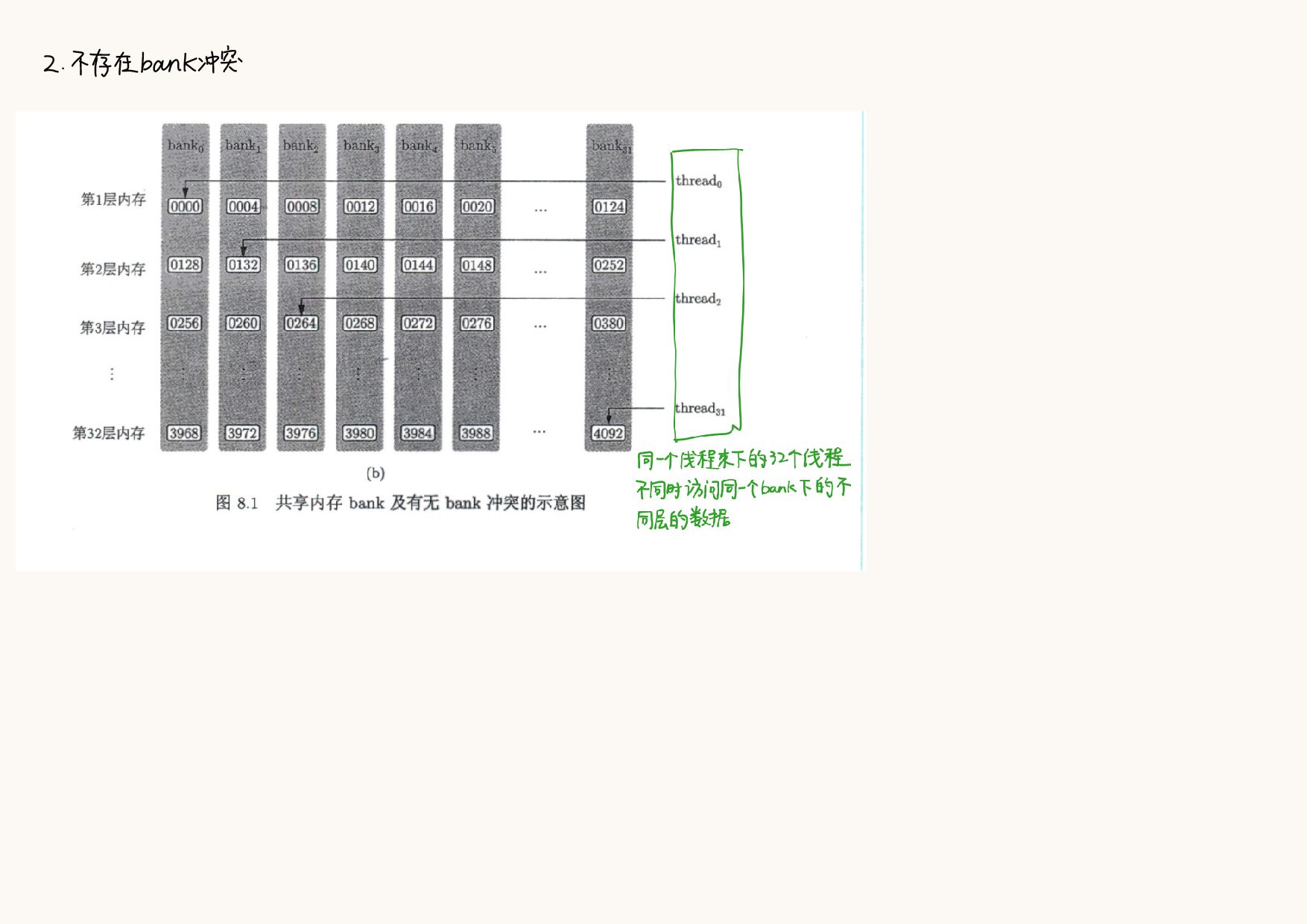
}8.3 避免共享内存的bank冲突
为了获得高的内存带宽,共享内存在物理上被分为32个(刚好等于一个线程束中的线程数目32)同样宽度的、能被同时访问的内存bank
- 单精度👇
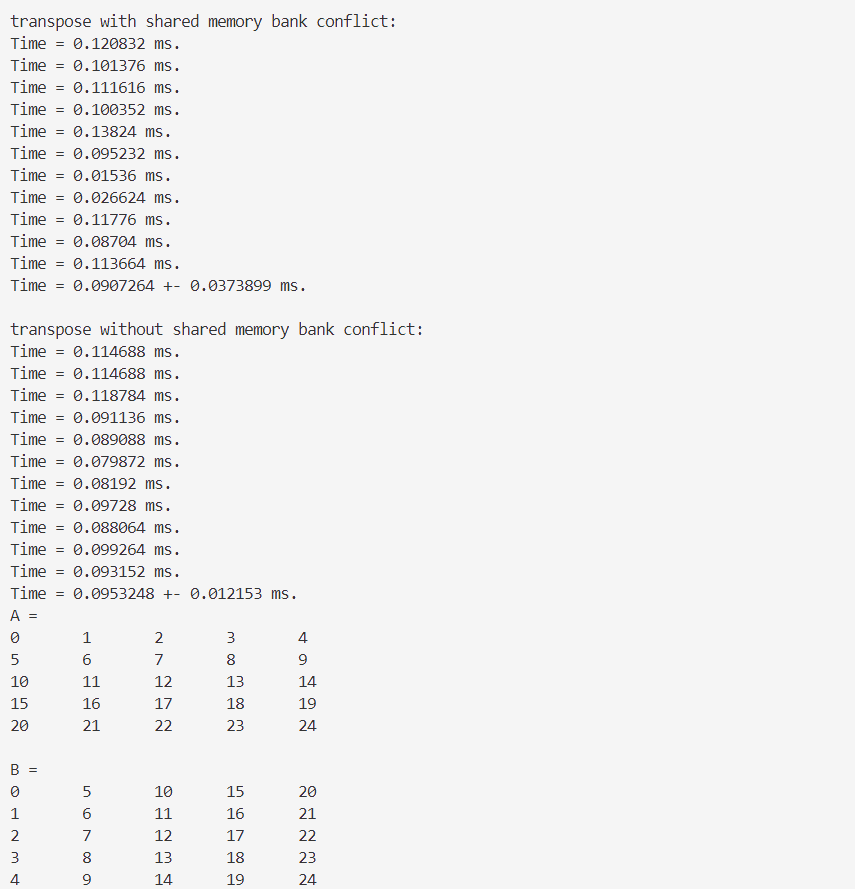
- 双精度👇
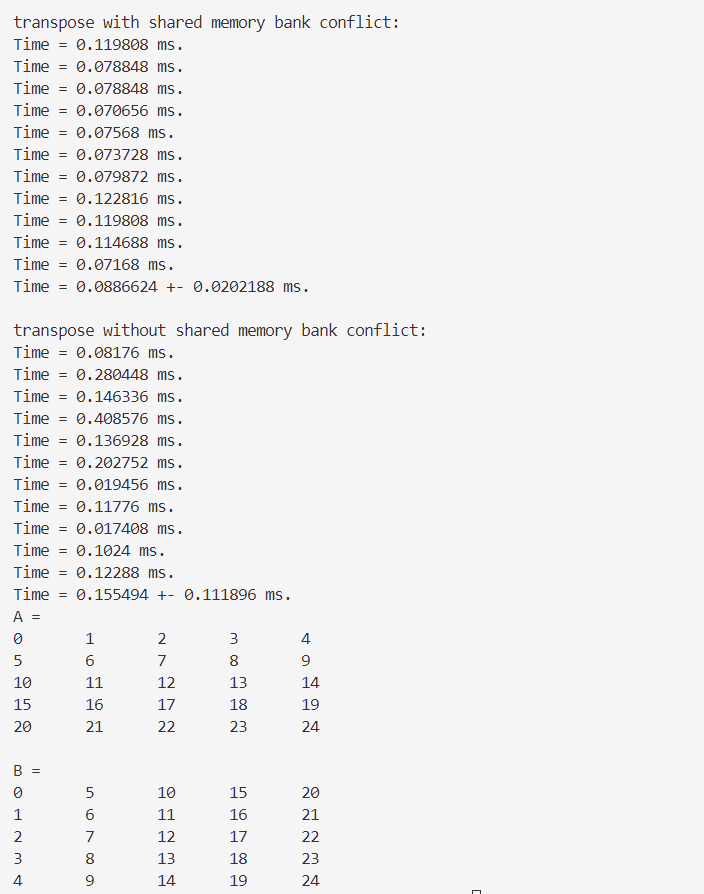
bank宽度为4字节的架构,$\dfrac{128字节(定义的共享内存数组的大小)}{32bank(大小和一个线程束中的线程数目相同)}=4字节/bank$ - 只要同一个线程束内的多个线程不同时访问同一个
bank中不同层的数据,该线程束对共享内存的访问就只需要一次内存事务 - 当同一线程的多个线程数试图访问同一个
bank中不同层(n层)的数据(将导致n次内存事务),会发生bank冲突(n路bank冲突) - 上面的
transpose with shared memory bank conflit是发生了32路bank冲突B[nx2 * N + ny2] = S[threadIdx.x][threadIdx.y]- 同一个线程束的32个线程(连续的32个
threadIdx.x值)对应S中跨度为32的数据([threadIdx.y])
- 于是将
__shared__ real S[TILE_DIM][TILE_DIM]改为__shared__ real S[TILE_DIM][TILE_DIM + 1]
9.1 完全在GPU中进行归约
- 本书使用在先前的核函数的末尾利用原子函数进行归约直接得到最终的结果的方法
- 不能使用👇的原因:不管每个线程块第0号线程的执行次序如何,只有当一个线程的“读-写”操作不被其他线程干扰时,才能得到正确结果
如果存在两个线程块第0号线程同时读取d_y[0]的值,那结果就是错误的if(tid == 0) { d_y[0] += s_y[0]; } - 原子函数
atomicAdd(address, val):- 第一个参数是待累加的变量的地址
- 第二个参数是累加的值
- “在调用该版本的核函数之前,必须将
d_y[0]的值初始化为0” - 👇
代码中:if(tid == 0) // threadIdx.x = 0,保证每个线程块的s_y[0]只累加一次 { atomicAdd(&d_y[0], s_y[0]);//&d_y[0]可以写成d_y(数组名是数组首个元素的地址) }d_x是长度为M的数组、N为元素个数
- 初始化
h_x,复制给d_x timing(d_x):- 重复
NUM_REPEATS次 - 创建事件、计时、查询
reduce(d_x)、- 定义网格大小
h_y[1]作用是传一个初始值为0的值给d_y,满足d_y[0]的值初始化为0的要求reduce(d_x, d_y, N):动态内存<<<grid_size, block_size, sizeof(real) * block_size>>>- 使用动态内存进行折半相加
- 使用
atomicAdd对每个线程块的首个元素相加得到最终结果
- 将结果从
d_y复制回h_y中 - 释放内存
- 结束计时,打印计时结果和最后一次的求和结果
- 重复
- 释放
d_x和h_x的内存
单精度👇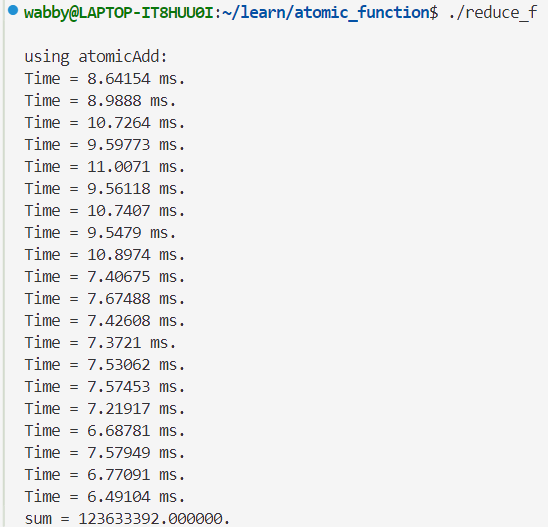
双精度👇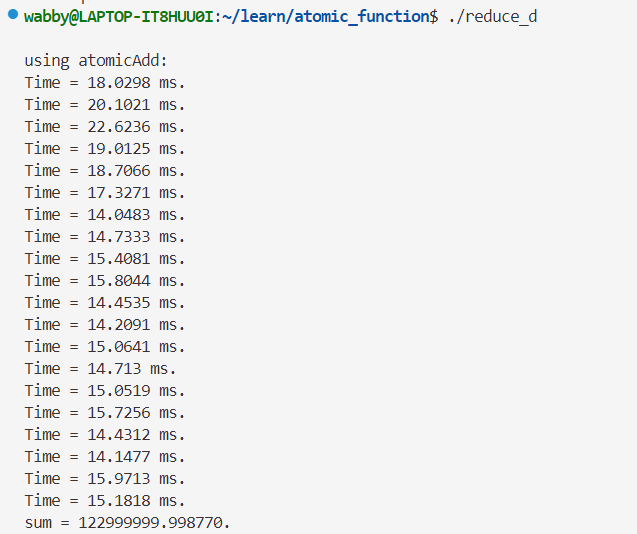
确实是比先前的提升约2ms
9.3 例子:邻居列表的建立
MN是每个原子的最多邻居原子数NN[n]是第n个粒子的邻居个数NL[n * MN + k]是第n个粒子的第k个邻居的指标
9.3.1 C++版本的开发
void find_neighbor(int *NN, int *NL, const real* x, const real* y)
{
for(int n = 0; n < N; n++)
{
NN[n] = 0;
}
// n1和n2代表两个可能互为邻居的原子
for(int n1 = 0; n1 < N; ++n1)
{
real x1 = x[n1];
real y1 = y[n1];
for(int n2 = n1 + 1; n2 < N; ++n2) // 因为n1和n2互为邻居,所以只考虑n2>n1的情形
{
real x12 = x[n2] - x1;
real y12 = y[n2] - y1;
real distance_square = x12 * x12 + y12 * y12; //
if(distance_square < cutoff_square)
{
NL[n1 * MN + NN[n1]++] = n2; // 先添加邻居信息,再对邻居个数++
NL[n2 * MN + NN[n2]++] = n1;
}
}
}
}9.3.2 利用原子操作的CUDA版本
如果仍然使用9.3.1中的find_neighbor函数,会导致“并发写入冲突”
一个线程与一个原子对应
- 与n1对应的线程👇
d_NL[n1 * MN + NN[n1]++] = n2; d_NL[n2 * MN + NN[n2]++] = n1; // 第二条语句 - 与n2对应的线程👇
书上原话“在与d_NL[n2 * MN + NN[n2]++] = n1; // 第一条语句 d_NL[n1 * MN + NN[n1]++] = n2;n1对应的线程中,第二条语句代表我们试图对d_NN[n2]进行累加操作。但是,在与n2对应的线程中,第一条语句代表我们也试图对d_NN[n2]进行累加操作”
需要用原子函数:d_NL[n1 * MN + d_NN[n1]++] = n2; d_NL[n2 * MN + d_NN[n2]++] = n1;
合理利用返回值:
可以将👇代码
NL[n1 * MN + NN[n1]++] = n2;
NL[n2 * MN + NN[n2]++] = n1;改写为👇
NL[n1 * MN + NN[n1]] = n2;
NN[n1]++;
NL[n2 * MN + NN[n2]] = n1;
NN[n2]++;但如果类似地改写原子函数的代码:
d_NL[n1 * MN + atomicAdd(&d_NN[n1], 1)] = n2;
d_NL[n2 * MN + atomicAdd(&d_NN[n2], 1)] = n1;👆改写为👇
d_NL[n1 * MN + d_NN[n1]] = n2;
atomicAdd(&d_NN[n1], 1);
d_NL[n2 * MN + d_NN[n2]] = n1;
atomicAdd(&d_NN[n2], 1);- 原子函数的操作本身是立即生效的,且在原子操作的执行过程中其他线程无法同时修改该变量
- 不同的线程可能会同时访问
d_NN[n1]和d_NN[n2],如果两个线程几乎同时执行对d_NN[n1]的atomicAdd操作,那么尽管操作本身是原子的,它们的执行顺序却是不确定的,一个线程可能在另一个线程更新d_NN[n1]之前就读到了该值
正确写法👇
使用临时变量int tmp1 = atomicAdd(&d_NN[n1], 1); d_NL[n1 * MN + tmp1] = n2; int tmp2 = atomicAdd(&d_NN[n2], 1); d_NL[n2 * MN + tmp1] = n1;tmp1和tmp2保存d_NN[n1]和d_NN[n2]的旧值
单精度👇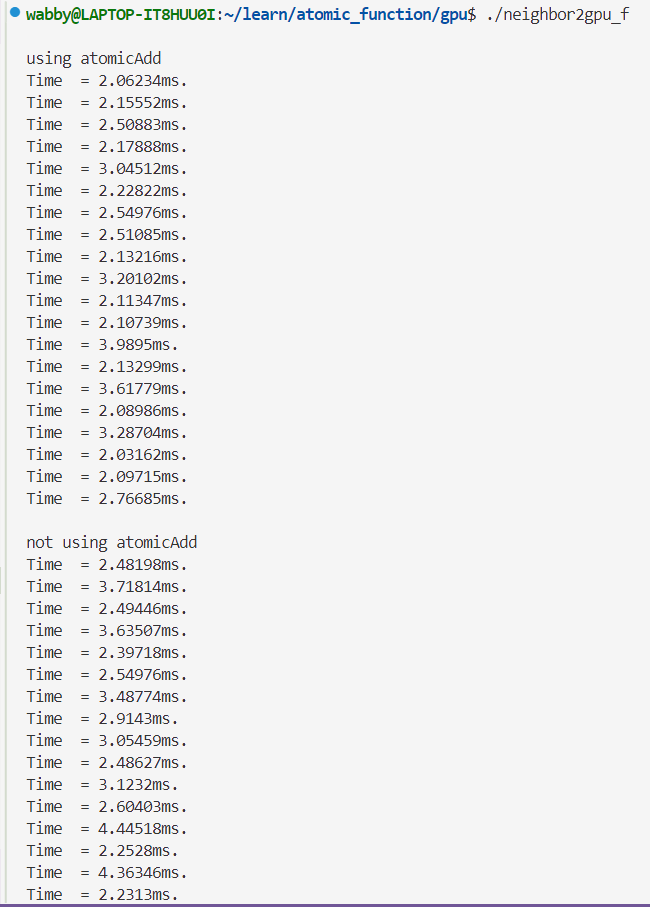
双精度👇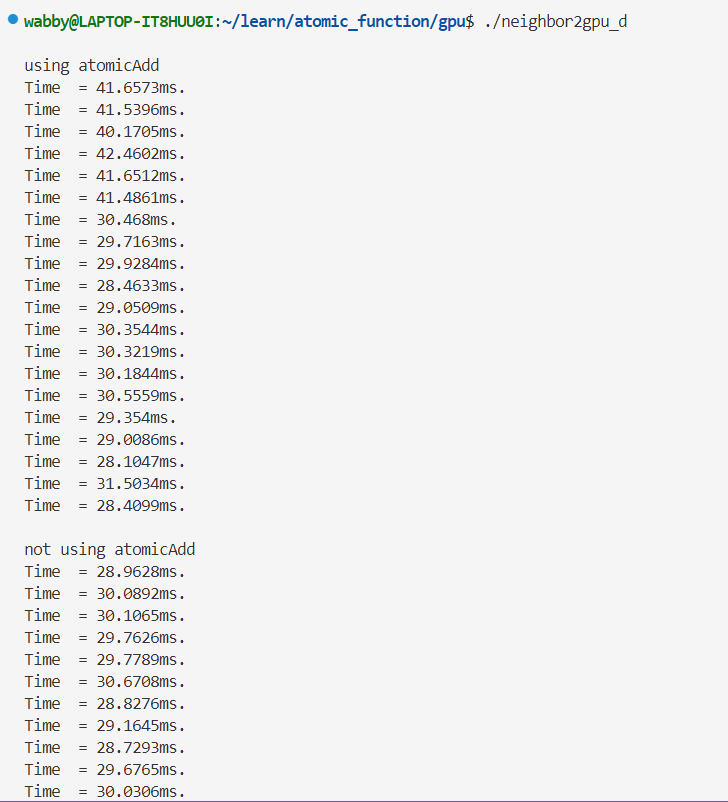
在核函数find_neighbor_no_atomic中,
①将d_NL[n1 * MN + count++]改为d_NL[(count++) * N + n1]
②const int n1 = blockIdx.x * blockDim.x + threadIdx.x;
- 前者的索引中:每个线程的地址跨度为
MN - 后者的索引中:每个线程在每次循环时访问相邻的内存位置
对于find_neighbor_not_atomic
①将if((distance_square) < cutoff_square && (n2 != n1))
改为if((n2 != n1) && (distance_square) < cutoff_square),用时变多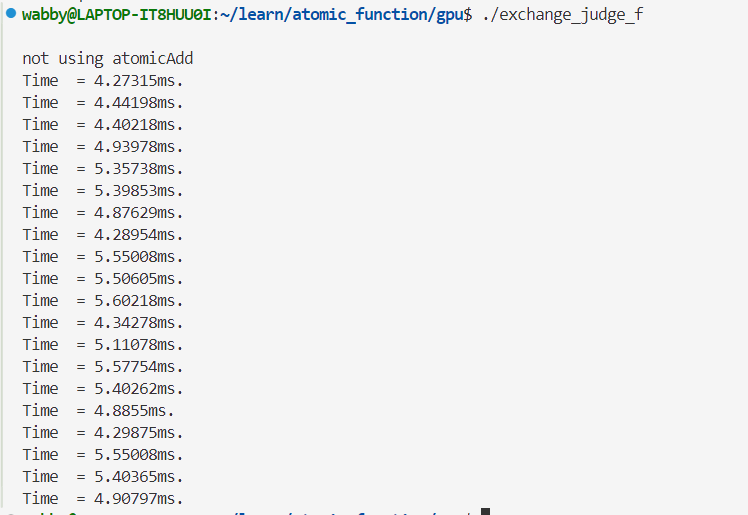
对比使用寄存器变量与不使用寄存器变量
使用👇
不使用👇,用时变多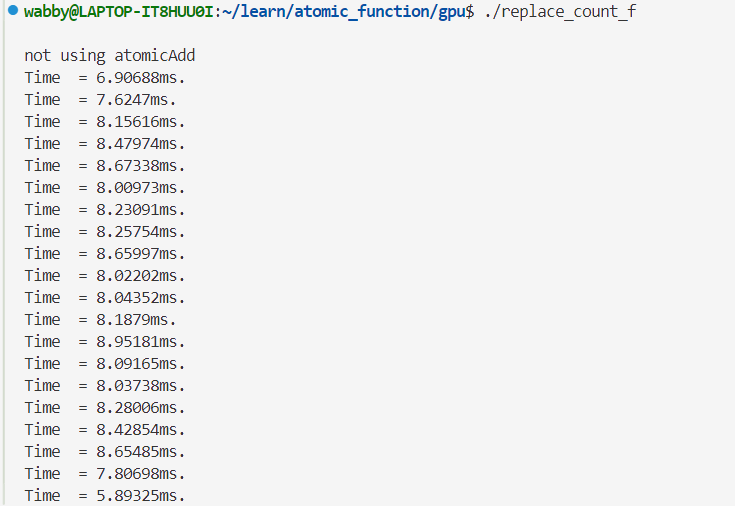
第十章 线程束基本函数与协作组
10.1 单指令-多线程执行模式
并发和同步:
- 并发:侧重任务的(逻辑)同时进行,在同一段时间内多个任务交替进行
- 同步:侧重控制人物的执行顺序,保证它们在合适的时刻访问共享资源
单指令-多线程:同一时刻,一个线程束中的线程只能执行一个共同的指令或者闲置
分治发散:一个线程束中的线程顺序地执行判断语句中的不同分支(分支是依次执行的)
一个SM可以处理一个或多个线程块,一个线程块不会被分配到不同的SM中
一个线程块可以氛围若干线程束
10.3 更多线程束内的基本函数
mask为掩码,是一个32位的无符号整数,用于指定要参与计算的线程,掩码中的一个二进制位为0/1代表对应的线程参与/不参与计算
①__ballot_sync(mask, predicate):返回一个新的掩码
mask先决定线程束内第n(n=1~32)个线程是否参与计算(0/1)predicate用于判断参与计算的线程是否满足条件,如果满足则该线程对应的predicate为1,对应的mask取1的比特位,否则对应的predicate为0,对应的mask取0
②__all_sync(mask, predicate):返回0/1
- 线程束内所有参与的线程对应的
predicate值都不为0才返回1,否则返回0 - 类似于选举操作,所有参选人都同意时通过
- 例:
int result = __all_sync(FULL_MASK, tid);如果所有线程的tid都为真(非零),函数返回 1,表示条件对所有线程都满足;否则返回 0,表示至少有一个线程的tid为零。
- 例:
③__any_sync(mask, predicate):返回0/1
- 线程束内所有参与的线程对应的
predicate值只要有一个不为0就返回1,如果全是0才返回0 - 类似选举操作,只要有一个参选人同意就通过
④__shfl_sync(mask, var, srcLane, width);每个子组中参与的线程获取land_id为srcLane的线程中的变量
land_id = threadIdx.x % w; = threadIdx.x & (w - 1);mask:表示线程束内参与的线程var:表示当前线程的变量srcLane:表示从哪个线程索引读取v的值width:表示参与这个shuffle操作的warp的宽度- 例:
__shfl_sync(FULL_MASK, tid, 2, 8)8表示__shfl_sync()操作只在8个线程的小组中进行,对于32线程的wrap,线程被分为4组有8个线程的子组(0-7, 8-15, 16-23, 24-31)2表示源线程索引,每个线程都会读取第2号线程的tid值并存到value变量中tid表示每个线程的局部变量__global__ void shuffleExample() { int tid = threadIdx.x % 32; // 假设每个线程的tid是线程索引(0~31) int value = __shfl_sync(0xFFFFFFFF, tid, 2, 8); printf("Thread %d got value %d\n", tid, value); } //打印结果👇 Thread 0 got value 2 Thread 1 got value 2 Thread 2 got value 2 Thread 3 got value 2 Thread 4 got value 2 Thread 5 got value 2 Thread 6 got value 2 Thread 7 got value 2 Thread 8 got value 10 Thread 9 got value 10 Thread 10 got value 10 Thread 11 got value 10 ... Thread 30 got value 26 Thread 31 got value 26
- 例:
- 将一个线程中的数据广播到所有(包括自己)线程
⑤__shfl_up_sync(mask, var, delta, width);
delta:表示每个线程从前面多少个线程处获取数据width:决定了warp内的分组范围,通信只在指定大小的组内进行- 例:
__shfl_up_sync(mask, var, 1, 8);
- 例:
vat:决定获取的数据来源
| 线程ID | tid | 执行后的tid |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 0 |
| 2 | 2 | 1 |
| 3 | 3 | 2 |
- 是一种将数据向上平移的操作
⑥__shfl_down_sync(mask, var, delta, width);
- 是一种将数据向下平移的操作
⑦__shfl_xor_sync(mask, var, landMask, width);
线程i与线程i ^ landMask(这里表示异或)交换数据
例子:landMask=1、width=8
| 线程ID | tid | 执行后的tid |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
| 2 | 2 | 3 |
| 3 | 3 | 2 |
| 4 | 4 | 5 |
| 5 | 5 | 4 |
| 6 | 6 | 7 |
| 7 | 7 | 6 |
| 8 | 8 | 9 |
| 9 | 9 | 8 |
| 10 | 10 | 11 |
| 11 | 11 | 10 |
| 12 | 12 | 13 |
| 13 | 13 | 12 |
| 14 | 14 | 15 |
| 15 | 15 | 14 |
以__shlf开头的函数为洗牌函数,好处是使得线程束中的线程彼此之间可以直接交换数据,而不是通过共享内存或全局内存来进行的。洗牌指令比共享内存有更低的延迟,并且该指令在执行数据交换时不消耗额外的内存

all_sync(FULL_MASK):0,线程0的tid为0,不是全部参与的线程的predicate值都为1,所以为0all_sync(mask1):1,线程0没有参与,全部参与的线程的predicate值都为1,所以为1any_sync(FULL_MASK):1,线程0的tid为0,只要参与的线程的predicate值至少有一个为1则为1,所以为1any_sync(mask2):1,线程0的tid为0,参与的线程的只有线程0,predicate值只有0,所以为0
10.3.2 利用线程束洗牌函数进行规约计算
real y = s_y[tid]; // 将共享内存中的数据复制到寄存器,在线程束内使用洗牌函数进行归约时,不需要明显地使用共享内存
for(int offset = 16; offset > 0; offset >>= 1)
{
y += __shfl_down_sync(FULL_MASK, y, offset); // y是读取的值,offset是向后移的个数
}
if(tid == 0)
{
atomicAdd(d_y, y);
}👆理解:
- 将共享内存中的数据复制到寄存器,在线程束内使用洗牌函数进行归约时,不需要明显地使用共享内存
- 洗牌函数先读取各个线程中y的值,再将洗牌操作的结果写入各个线程的y中
- 假设
y(tid = n) = n- `offset=16
y(tid=0) += __shfl_down_sync(FULL_MASK, y(tid=0), offset);y(tid=0) = 0__shfl_down_sync() -> y(tid=0)' = y(tid=16) = 16,'表示后来的y(tid=0) = y(tid=0) + y(tid=0)' = 0 + 16 = 16
y(tid=1) = 1 + 17 = 18- …
y(tid=15) = 15 + 31 = 46
offset=8y(tid=0) = y(tid=0) + y(tid=7)- …
offset=1y(tid=0) = y(tid=0) + y(tid=1)
- `offset=16
- 假设
10.4 协作组
协作组:看作线程块和线程束同步机制的推广
- 使用协作组的功能时需要在相关源文件包含如下头文件:
#include<cooperative_groups.h> - 导入命名空间
cooprtative_groups中的内容:using namespace cooperative_groups;
定义并初始化一个thread_block对象:thread_block g = this_thread_block();,g就代表了线程块
- 等价关系:
g.sync()↔__syncthreads()g.group_index()↔blockIdxg.thread_index()↔threadIdx
tiled_partition()将一个线程块分为若干片(tile),每一片构成一个新的线程组,大小只能是2、4、8、16、32
- 模板化:
thread_block_tile<32> g32 = tiled_partition<32>(this_thread_block());thread_block_tile<4> g4 = tiled_partition<4>(this_thread_block());
这样定义的线程组称为线程块片,线程块片函数不同的地方: - 线程组内的所有线程都必须参与相关函数的运算
- 宽度就是线程块片的大小
real y = s_y[tid];
thread_block_tile<32> g = tiled_partition<32>(this_thread_block());
for(int i = g.size() >> 1; i > 0; i >>= 1)
{
y += g.shfl_down(y, i);
}
if(tid == 0)
{
atomicAdd(d_y, y);
}把线程划分32个线程一组的,其他的与洗牌函数的步骤差不多,只是使用的方法不一样,所以他们两种方法的用时也差不多
单精度👇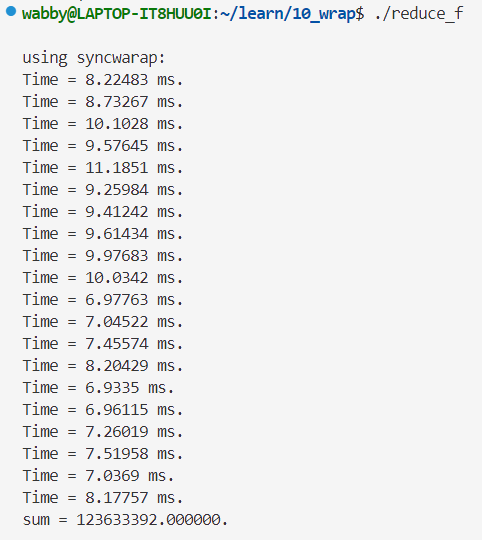
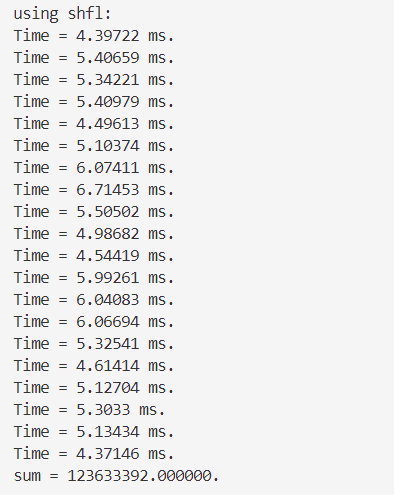
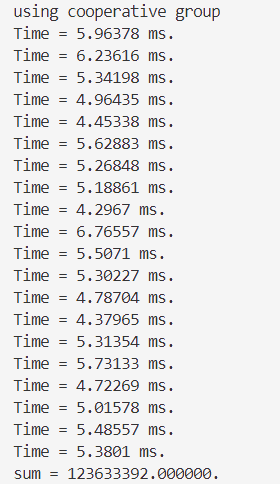
双精度👇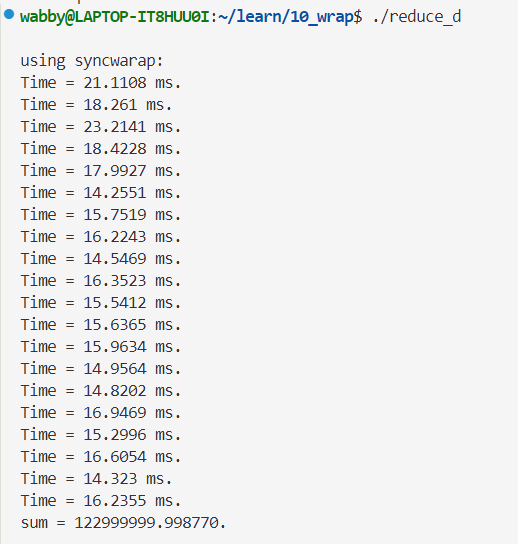
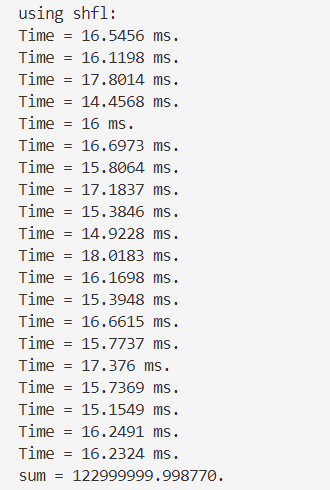
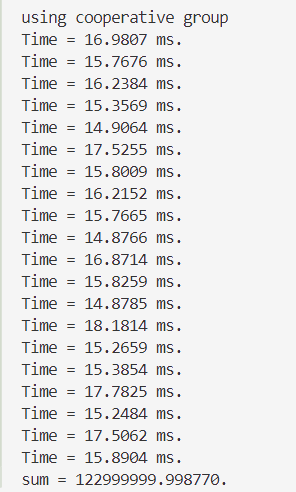
10.5 数组规约程序的进一步优化
10.5.1 提高线程利用率
“如果能够提高归约之前所做计算的比例,则应该可以从整体上升对线程的利用率…,可以在归约之前将多个全局内存数组的数据累加到一个共享内存数组的一个元素中”
“不要让一个线程处理相邻的若干数据,因为这必然导致全局内存的非合并访问”,如何理解这句话(这句话本人读了好一会才理明白):
- 什么是合并访问?
- $合并度=\dfrac{线程束请求的字节数}{由该请求导致的所有数据传输处理的字节数}$
- 合并访问就是合并度100%的情况,注意:线程的组织情况是以线程束为单位
- 为什么一个线程处理会导致非合并
- (以下是带有主观的解释)一个线程处理相邻的数据,如
tid=0 -> 访问 d_x[0], d_x[1], d_x[2], d_x[3]tid=1 -> 访问 d_x[4], d_x[5], d_x[6], d_x[7]- 在一个线程束内,每一时刻每个线程访问的数据不是连续的(
d_x[tid * 4]),数据的传输的首地址某个最小颗粒度的倍数 - 假设需要请求的数据为
d_x[0]~d_x[31],每个元素大小为4字节,某个最小颗粒度为32 - 在第一个时刻中,
tid = 0 -> 0 ... tid = 7 -> 28 - 在第二个时刻中,
tid = 0 -> 1 ... tid = 7 -> 29 - 在第三个时刻中,
tid = 0 -> 2 ... tid = 7 -> 30 - 在第四个时刻中,
tid = 0 -> 3 ... tid = 7 -> 31 - $合并度=\dfrac{线程束请求的字节数}{由该请求导致的所有数据传输处理的字节数}=\dfrac{128}{128*4}=\dfrac{1}{4}$,4是代表进行了4次从0~128字节的访问(即
d_x[0]~d_x[31])
- 怎么样访问才是合并的?
- 相邻线程访问连续的地址,例子见第七章第一节的顺序的合并访问
单精度👇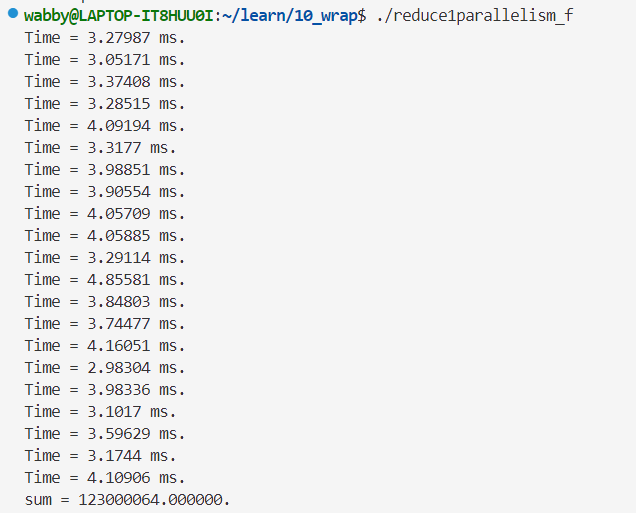
双精度👇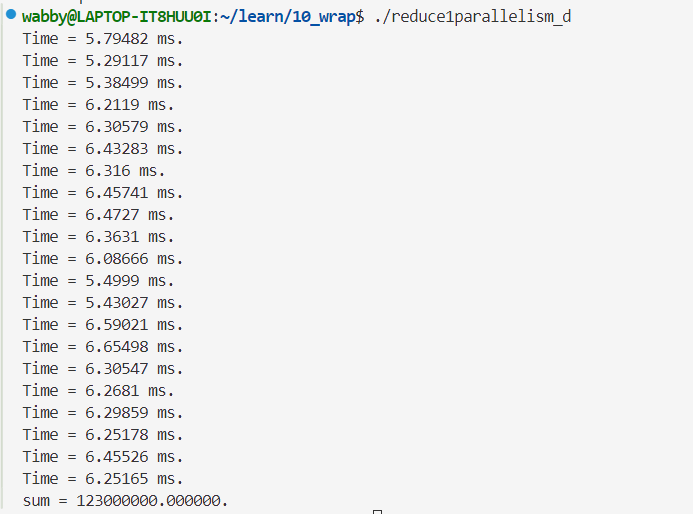
可以发现优化后在时间和精度上都有所提升!
reduce_cp<<<GRID_SIZE, BLOCK_SIZE, smem>>>(d_x, d_y, N);
reduce_cp<<<1, 1024, sizeof(real) * 1024>>>(d_y, d_y, GRID_SIZE); // 有GRID_SIZE个块需要归约- 用
d_y[bid] = y;代替了atomicAdd(d_y, y) - 使用两个核函数可以获得更加精确的结果,这是因为使用两个核函数时,将数组
d_y归约到最终结果的计算使用了折半求和,比直接累加(使用原子函数或复制到主机再累加的情况)更稳健
10.5.2 避免反复分配与释放设备内存
在10.5.1的reduce()函数中,需要为数组d_y分配与释放设备内存。实际上,设备内存的分配与释放是比较耗时的
real reduce(const real* d_x)
{
const int ymem = sizeof(real) * GRID_SIZE;
...
CHECK(cudaMalloc(&d_y, ymem)); // 分配内存
...
CHECK(cudaFree(d_y)); // 释放内存
}解决方法:使用静态全局内存代替动态全局内存,因为静态内存在编译期间就会分配好
- 定义静态全局内存变量:
__device__ real static_y[GRID_SIZE]; - 在不改变核函数代码的情况下,可以用
cudaGetSymbolAddress()获得一个指向该静态全局内存的指针__device__ real static_y[GRID_SIZE]; real reduce(const real* d_x) { real* d_y; CHECK(cudaGetSymbolAddress((void**)&d_y, static_y)); //将指向d_y的指针指向static_y const int smem = sizeof(real) * BLOCK_SIZE; reduce_cp<<<GRID_SIZE, BLOCK_SIZE, smem>>>(d_x, d_y, N); reduce_cp<<<1, 1024, sizeof(real) * 1024>>>(d_y, d_y, GRID_SIZE); real h_y[1] = {0}; CHECK(cudaMemcpy(h_y, d_y, sizeof(real), cudaMemcpyDeviceToHost)); return h_y[0]; }cudaGetSymbolAddress(void** devPtr, const char* symbol); void*8 devPtr:是一个指向指针的指针,函数会修改这个指针,使其指向指定符号在设备上的地址const char* symbol:是一个字符串,表示你想要获取地址的符号名称(通常是全局变量或常量变量的名称,需要以__device__或__constant__存储类定义)- 使用场景:在设备中定义了一个全局变量或常量,并希望在内核或其他CUDA函数中使用
- 示例👇
// 定义 __device__ float static_y; // 获取static_y的地址 float *d_y; cudaGetSymbolAddress((void**)&d_y, "static_y");
单精度👇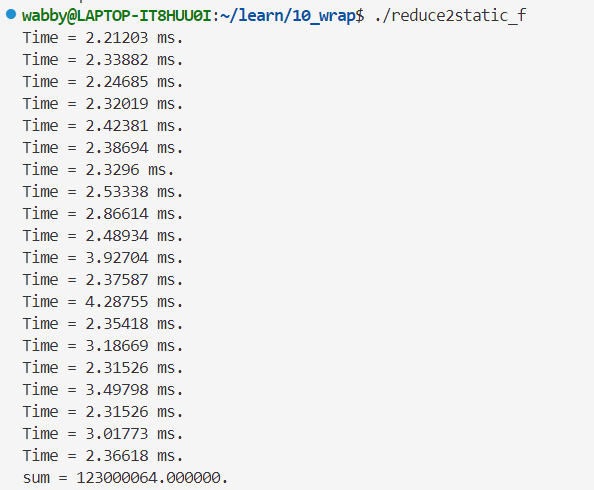
双精度👇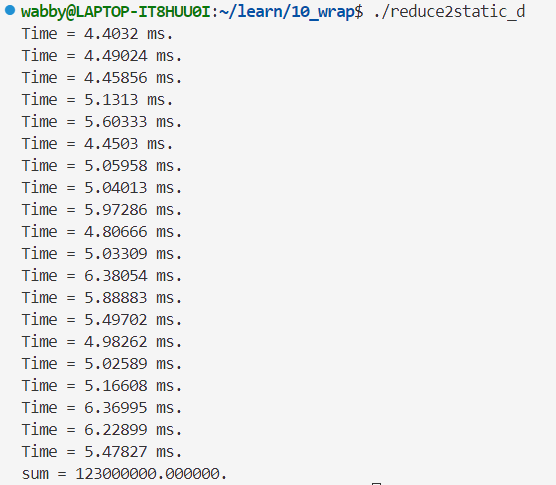
用时比使用动态全局内存更短!
第十一章 CUDA流
核函数外部的并行主要指:
- 核函数计算与数据传输之间的并行
- 主机计算与数据传输之间的并行
- 不同的数据传输之间的并行(cudaMemcpy函数中的第四个参数)
- 核函数计算与主机计算之间的并行
- 不同核函数之间的并行
一般来说,要获得较高的加速比,如要减少主机与设备之间的数据传输及主机中的计算,尽量在设备中完成所有计算
11.1 CUDA流概述
一个CUDA流指的是由主机发出的在一个设备中执行的CUDA操作(即和CUDA有关的操作,如主机-设备数据传输和核函数执行)序列
CUDA流:
- 默认流(空流)
- 非默认流(非空流)
- 在主机端产生和销毁
- 一个CUDA流由类型为
cudaStream_t的变量表示 - 产生:
cudaStreamCreate(cudaStream_t*),输入参数是cudaStream_t类型的指针 - 销毁:
cudaStreamDestroy(cudaStream_t*),输入参数cudaStream_t类型的变量 - 检查一个CUDA流中的所有操作是否都在设备中执行完毕:
cudaStreamSynchronize(cudaStream_t stream),cudaStreamSynchronize()会强制阻塞主机,直到CUDA流stream中的所有操作都被执行完毕cudaStreamQuery(cudaStream_t stream),cudaStreamQuery()不会阻塞主机,只是检查CUDA流stream中的所有操作是否都执行完毕
11.2 在默认流中重叠主机和设备计算
cudaMemcpy(d_x, h_x, M, cudaMemcpyHostToDevice); // 主机发出命令后,需等待命令执行完毕才执行下一步,在等待的过程中主机闲置
cudaMemcpy(d_y, h_y, M, cudaMemcpyHostToDevice); // 主机发出命令后,需等待命令执行完毕才执行下一步,在等待的过程中主机闲置
sum<<<grid_size, block_size>>>(d_x, d_y, d_z, N); // 主机发出命令后,不会等待该命令执行完毕,主机紧接着会发出下一条指令
cudaMemcpy(h_z, d_z, M, cudaMemcpyDeviceToHost); // 因为这是默认流中的CUDA操作,必须等待前一个CUDA操作执行完毕才会执行这条命令👆CUDA操作例子(注释是主机角度)
从设备角度看:上面4个CUDA操作在默认的CUDA流中按代码出现的顺序依次执行
从主机角度看:
①主机在发出核函数命令的调用后会立刻发出下一个命令
②(1)如果下一个命令是数据传输,从设备角度看必须等待核函数执行完毕(实际上主机也在等执行完毕)
②(2)如果下一个命令是主机中的某个计算任务,那么主机会在设备执行核函数时同时进行一些计算,这样主机和设备就可以同时进行(设备完全不知道在它执行核函数时,主机偷偷地做了些计算)
实践(结果和书上的不符合):
- 采用单精度浮点数,在数据量一样时,核函数
gpu_sum比主机端函数cpu_sum约快10倍,因此设置$ratio=\dfrac{设备端函数所处理的数据量}{主机端函数所处理的数据量}$,使得gpu_sum和cpu_sum执行时间差不多 - 这里的结果和书上的不太符合(思考.jpg)
结果(书上的):
- 当主机函数和设备函数的计算量相当时,将主机函数放在设备函数之后(GPU -> CPU)可以达到主机函数与设备函数并发执行的效果,从而有效地隐藏主机函数的执行过程
- 如果主机函数和设备函数计算时间差很多,加速效果不显著
11.3 用非默认CUDA流重叠多个核函数的执行
同一个CUDA流中的CUDA操作在设备中是顺序执行的(非并行),那么同一个CUDA流中的核函数也必须在设备中顺序执行,如果要实现多个核函数之间的并行必须使用多个CUDA流
核函数的调度方式my_kernel<<<N_grid, N_block>>>(); -> 在默认流执行my_kernel<<<N_grid, N_block, N_shared>>>(); -> 在默认流执行my_kernel<<<N_grid, N_block, N_shared, stream_id>>>(); -> 非空流执行
N_grid是网格大小N_block是线程块大小N_shared是核函数中使用的动态共享内存的字节数stream_id是CUDA流的编号
可能是设备不同的问题,和书上的结果不太一样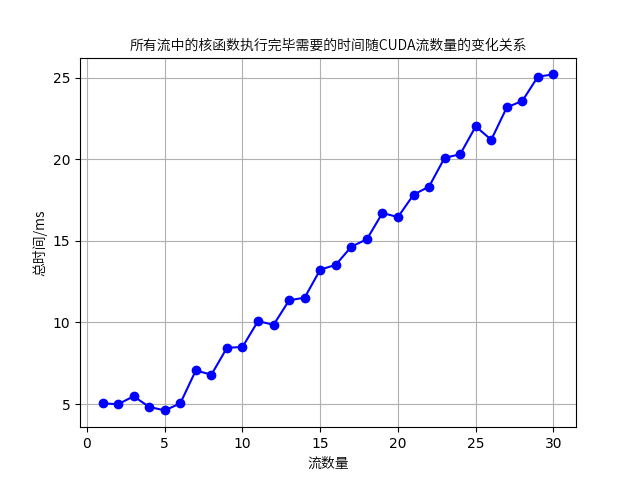
结果(书上的):
CUDA流并发多个核函数可以提升GPU硬件的利用率,减少闲置的SM,从而从整体上获得性能提升
11.4 用非默认CUDA流重叠核函数的执行与数据传递
若需要实现核函数执行与数据传输的并发(重叠)
- 必须让这两个操作处于不同的非默认流
- 数据传输需要使用异步版本
cudaMemcpyAsync()函数- 异步传输由GPU中的DMA(direct memory access)直接存储访问器,不需要主机参与
- DMA提供在外设和存储器之间或者存储器和存储器之间的高速数据传输
- 数据的复制和存储数据对于CPU来说没那么重要,可以交给DMA,解决大量数据转移过度消耗CPU资源的问题
- 如果用同步的数据传输函数
cudaMemcpy(),主机向一个流发出数据传输的命令后无法立刻获得控制权,必须等待数据传输完毕,即主机无法同时向另一个流调用核函数,也就不能实现核函数与数据传输的重叠 cudaMemcpyAsync(void *dst, const void *src, size_t count, enum cudaMemcpyKind kind, cudaStream_t stream)比cudaMemcpy()多一个参数,是所在流的变量- 在使用异步的数据传输时,需要将主机内存定义为不可分页内存或者固定内存
- 不可分页内存:若将主机内存声明为不可分页内存,则在程序运行期间其物理地址保持不变
- 系统操作有权在一个程序运行期间改变程序中使用的可分页主机内存的物理地址
- 异步传输由GPU中的DMA(direct memory access)直接存储访问器,不需要主机参与
不可分页主机内存的分配函数
cudaMallocHost(void **ptr, size_t size);cudaHostAlloc(void **ptr, size_t size, size_t flags);,如果第三个参数取默认值cudaHostAlllocDefault,则和上面的函数等价
不可分页主机内存的释放函数cudaFreeHost(void *ptr);
这里的时间是把前几次REPEAT次数的时间也加上了
| CUDA流=1 | 2 | 4 | 8 | 16 | 32 | 64 | |
|---|---|---|---|---|---|---|---|
| REPEAT次数=1 | 0.727245 | 0.813056 | 0.671984 | 0.633242 | 0.640717 | 0.732979 | 0.711456 |
| 2 | 1.48132 | 1.6044 | 1.29539 | 1.25809 | 1.2987 | 1.37727 | 1.40511 |
| 3 | 2.15654 | 2.40559 | 1.94911 | 1.89739 | 1.98509 | 2.0228 | 2.10539 |
| 4 | 2.90161 | 3.17943 | 2.62284 | 2.54855 | 2.64568 | 2.66245 | 2.8182 |
| 5 | 3.5848 | 3.97385 | 3.29006 | 3.16776 | 3.29783 | 3.32314 | 3.53272 |
| 6 | 4.2719 | 4.79479 | 3.97973 | 3.8308 | 3.96661 | 4.00003 | 4.19064 |
| 7 | 5.04011 | 5.60569 | 4.61964 | 4.49671 | 4.65433 | 4.62836 | 4.84917 |
| 8 | 5.90314 | 6.3983 | 5.27192 | 5.15115 | 5.28048 | 5.26508 | 5.52204 |
| 9 | 6.73892 | 7.15903 | 5.94195 | 5.7894 | 5.90922 | 5.90743 | 6.19399 |
| 10 | 7.55339 | 8.02287 | 6.58859 | 6.41499 | 6.53621 | 6.56247 | 6.8724 |
看起来并行效果是还不错的。
第十四章 CUDA标准库的使用
14.2 Thrust库
- Thrust库是一个实现了众多基本并行算法的C++模板库
- 该库中的所有类型与函数都在命名空间thrust中定义,所以用到
thrust::开头 - Thrust中有两种矢量:
thrust::host_vector<typename>,存储于主机中thrust::device_vector<typename>,存储于设备中thrust::devive_vectot<double> x(10, 0);,元素类型为双精度浮点数(全部初始化为0),长度为10
- 除了
thrust::copy,Thrust算法的参数必须都来自于主机矢量或都来自于设备矢量,否则编译器会报错
14.2.4 例子:前缀和
- 使用
device_vector来实现thrust::device_vector(int) x(N, 0); thrust::device_vector(int) y(N, 0);
- 扫描操作
thrust::inclusive_scan(x.begin(), x.end(), y.begin());thrust::inclusive_scan(InputIterator begin, InputIterator end, OutputIterator result);
InputIterator begin输入范围的起始迭代器。
InputIterator end: 输入范围的结束迭代器。
OutputIterator result: 用于存储结果的输出范围起始迭代器。
这里的迭代器可以理解为指针的推广
例子中使用了thrust::inclusive_scan(x.begin(), x.end(), y.begin()); - 输出
y是设备矢量,y[i]不是普通整型的变量,需要强制转化为整型后才能用printf()函数输出。用C++的输入/输出流可以直接输出y[i]而不需要先做强制类型转换
- 直接用设备中的数组(指针)实现
- 定义
cudaMalloc((void **)&x, sizeof(int) * N); cudaMalloc((void **)&y, sizeof(int) * N); 扫描操作
thrust::inclusive_scan(thrust::device, x, x + N, y);对于使用设备矢量的版本,该函数用了一个额外的表示执行策略的参数
thrust::device,需要包含头文件<thrust/execution_policy.h>如果大量使用Thrust库提供的功能,使用设备矢量
- 如果偶尔使用Thrust库提供的功能,使用设备指针
14.3 cuBLAS库
行主序和列主序,前者要求矩阵的每一行元素在内存中是连续的,后者以此类推
cuBLAS库包含3个API,其中一个为cuBLAS API,可以实现BLAS三个层级的函数
- 第一层函数处理矢量之间的运算
- 第二层函数处理矩阵和矢量之间的运算
- 第三层函数处理矩阵之间的运算
14.3.2 例子:矩阵乘法
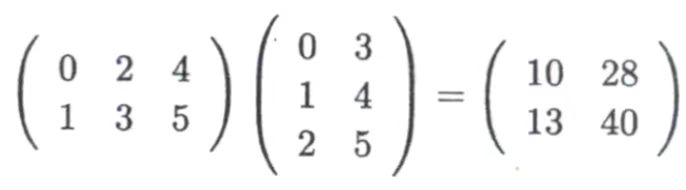
使用cuBLAS时使用<cublas_v2.h>作为头文件
在初始化h_A、h_B、h_C时用一维矢量来表示矩阵
- 主机数组和设备数组的复制
- 从主机数组复制到设备数组
cublasStatus_t cublasSetVector ( int n, int elemSize, cosnt void *x, int incx, void *y, int incy )n:复制的元素个数elemSize:每个元素的字节数incx/incy:表示对数组x/y进行访问时每incx/incy个数据中取一个x:主机数组y:设备数组
例:cublasSetVector(MK, sizeof(double), h_A, 1, g_A, 1); - 从设备数组复制到主机数组
cublasGetVector()其中参数相同,顺序不同
例:cublasGetVector(MK, sizeof(double), g_A, 1, h_A, 1);
- 矩阵乘法计算
- 定义一个
cublasHandle类型的变量并用cublasCreate()函数初始化 - 调用
cublasDgemm()函数做矩阵相乘的计算- 是第三层的
cuBLAS函数之一 D:doublegemm:GEneral Matrix-Matrix multiplication- 执行如下计算
C = alpha * transa(A) * transb(B) + beta * Ctransa(A)是对矩阵A做一个变换之后得到的矩阵,维度是m × ktransb(B)是对矩阵B做一个变换之后得到的矩阵,维度是k × nC的维度是m × ncublasDgemm ( cublasHandle_t handle, cublasOperation_t transa, cublasOperation_t transb, int m, int n, int k, const double *alpha, const double *A, int lda, const double *B, int ldb, const double *beta, double *C, int ldc );cublasOperation_t transa中transa为:
- 是第三层的
cuBLAS_OP_N,transa(A)等于AcuBLAS_OP_T,transa(A)等于A的转置cuBLAS_OP_C,transa(A)等于A的共轭转置lda、ldb和ldc分别是transa(A)、transa(B)和C的主维度,他们都是列主序,所以他们的主维度是矩阵的行数
最后的结果h_C是列主序的(10 13 28 40),打印时需要注意
补充Event
- 创建事件:首先使用
cudaEventCreate()创建事件对象。 - 记录事件:在需要记录的时间点调用
cudaEventRecord(event, stream)。 - 计算时间:通过
cudaEventElapsedTime()计算两个事件之间的时间差。 - 销毁事件:最后使用
cudaEventDestroy()销毁事件对象以释放资源。 - 同步:
cudaEventSynchronize(stop)会阻塞 CPU,直到 GPU 确保从start到stop之间的所有操作都完成了。这对于测量内核函数执行时间或在 CPU 侧进行同步非常重要。 - 检查事件是否完成:
cudaEventQuery(start)它的主要功能是检查指定的 CUDA 事件是否已经完成,而不需要阻塞主机线程。cudaEventQuery常用于需要频繁检查事件状态的场景。和cudaEventSynchronize不同,cudaEventQuery是非阻塞的,不会让 CPU 等待 GPU 任务完成,而只是检查 GPU 的执行状态。如果事件还未完成,它会立即返回cudaErrorNotReady,让程序可以继续执行其他任务。
补充运行
$nvcc -arch=_75 add1.cu -o add1,选择真实架构计算能力$nvcc -O3 -arch=_75 add1.cu -o add1,选择最激进的优化,生成最快的代码,但可能会增加编译时间和二进制文件大小。(C++程序的性能显著地依赖于优化选项)$nvcc -O3 -arch=sm_75 -DUSE_DP add1.cu -o add1使用if的选项,不写-DUSE_DP的话使用else的选项
补充C++语法
void read_xy(std::vector<real>& x, std::vector<real> y);:
std::vector:C++的动态数组,大小是动态的std::vector<real>& x:对于x是引用传递,在read_xy函数内部对x的任何修改,都会直接影响到他们本身(而不是副本),对外部的x也会有影响
std::ifstream infile("xy.txt");
std::ifstream:表示输入文件流,用于从文件读取数据infile:用来打开文件并读取内容
std::ofstream outfile("neighbor.txt");
std::ofstream:表示输出文件流,将数据写入到文件中
std::istringstream words(line);
std::istringstream:表示输入字符串流,可以从一个字符串中逐个提取数据words:从字符串中提取数据- 这段代码作用:使用
words来逐个读取line中的单词或数据