1 Image Classification

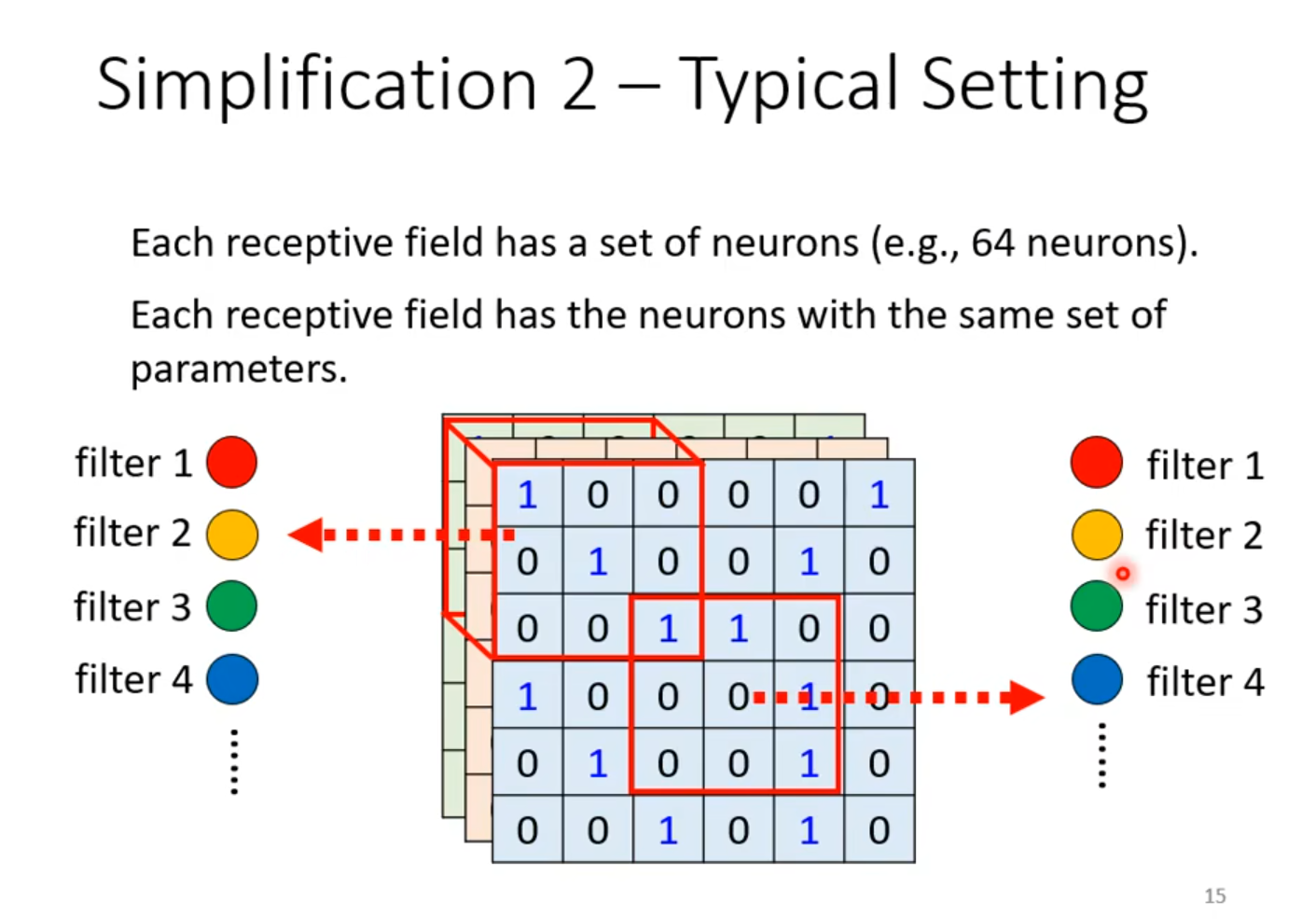
一张100x100pixels的图片其实是一个3D-tensor：
①图片的高100②图片的宽100③3 channelsRGB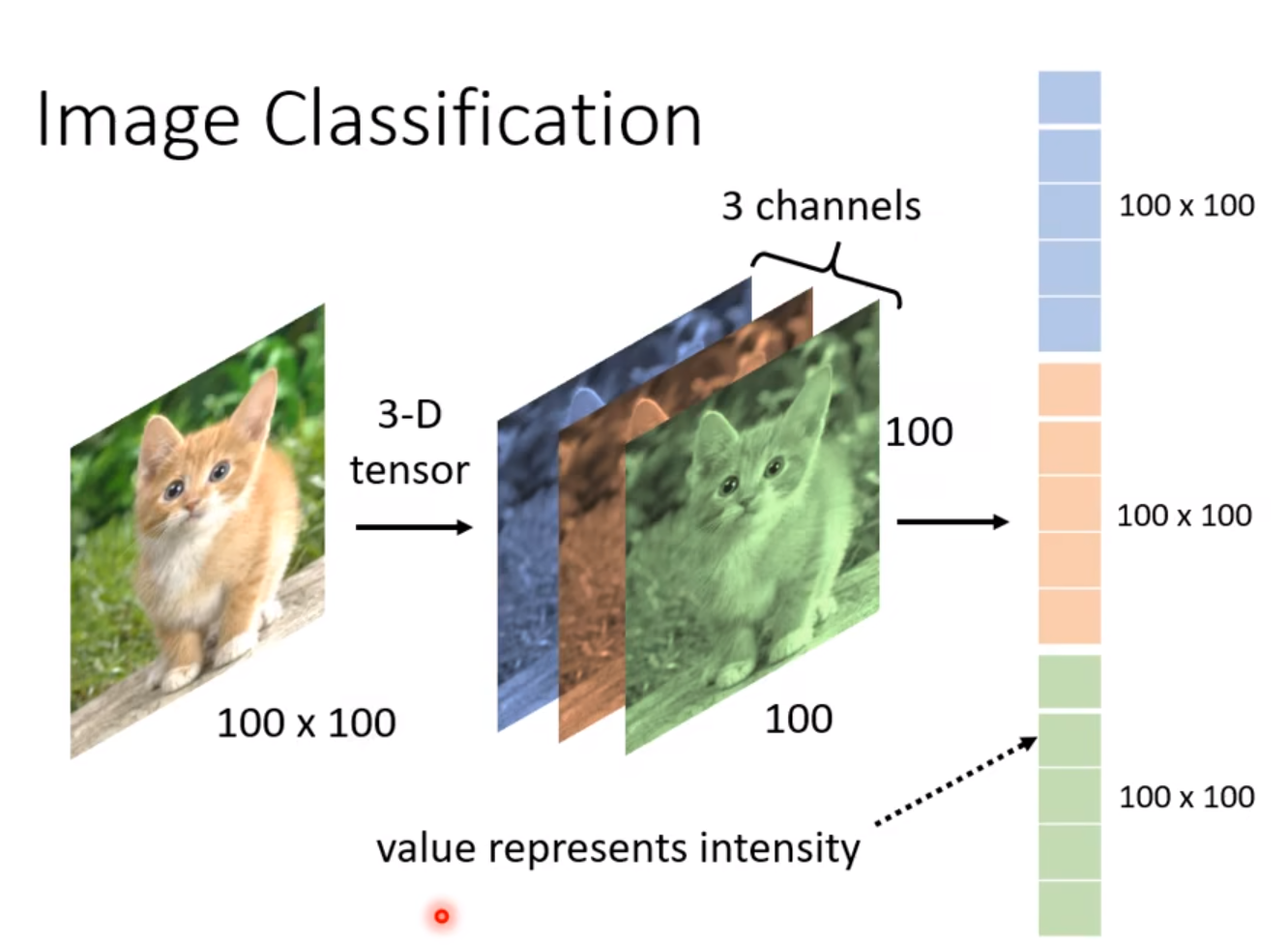

每一个数值代表某一个颜色某一个pixel的强度

2 Image Feature Observation

2.1 Observation 1

Identifying some critical patterns
比如说一只鸟，只用看鸟嘴、眼睛和脚也能大致辨认出来
A neuron does not have to see the whole image
Simplification
设定一个区域为Receptive field，每一个neuron只关心自己的Receptive field。
Receptive field can be overlapped
neuron can have the same receptive field
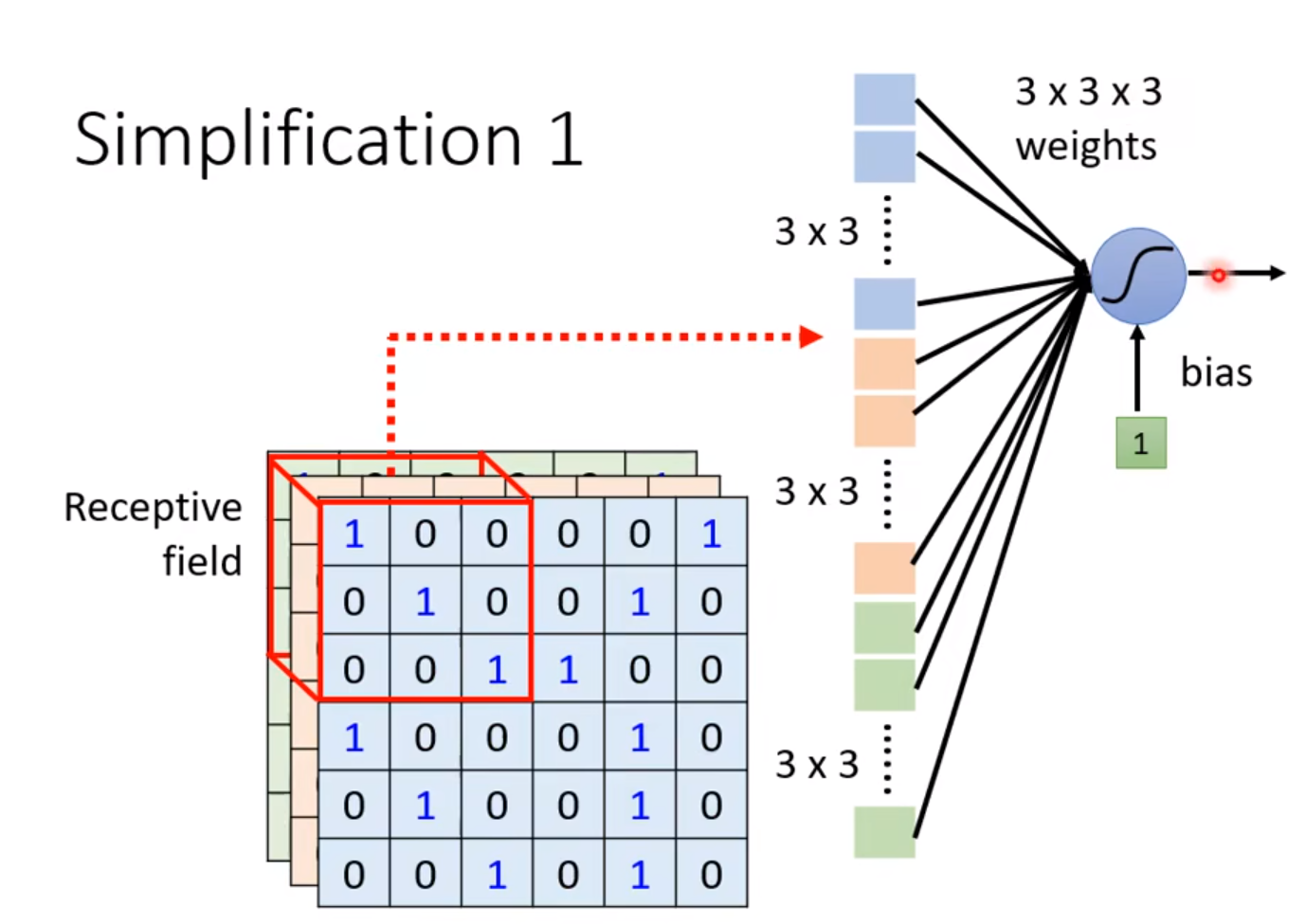
Simplification 1-Typical Setting
1. 会看all channels，不用提深度，高和宽合起来叫kernel size
2. Each receptive field has a set of neurons
3. 平移receptive field，步长为stride，receprive field有重叠，防止交界处有pattern没被neuron侦测到
4. 平移时超出范围了，用填补0代替超出的范围(方法不唯一)
  2.2 Observation 2

The same patterns appear in different regions
👇solution: parameter sharing

 线条代表weight，相同颜色代表weight一样，守备的receptive field不一样，参数一样，因为输入不一样，所以输出也不一样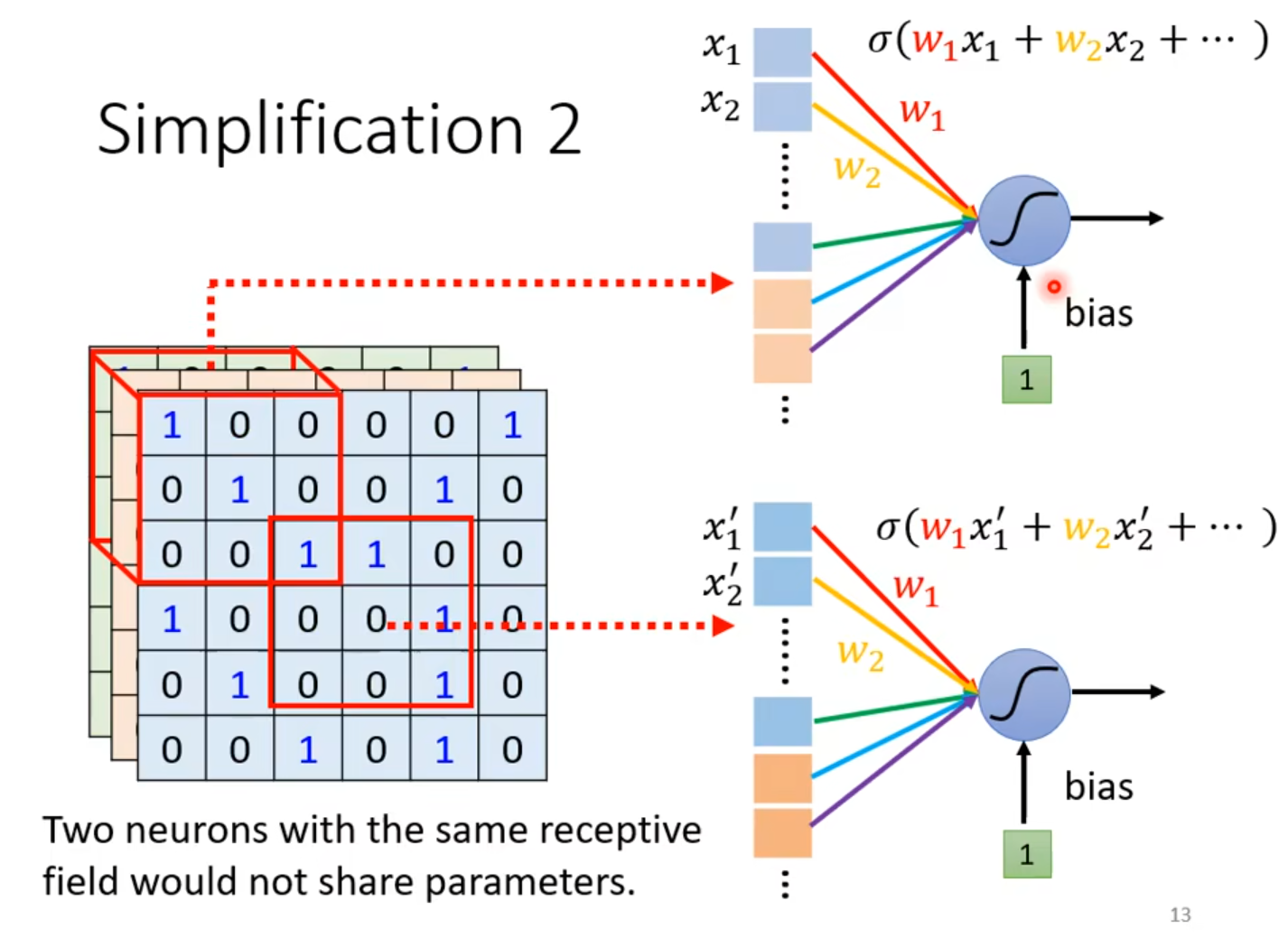

Simplification 2-Typical Setting
1. 每一个receptive field都有一组neurons
2. 相同颜色的圆圈代表共享一样的参数的neurons
3. 每一个receptive field都只有一组参数，这些参数叫filter x
  2.3 Obeservation 3
  Subsampling the pixels will not change the object
  e.g.拿掉image奇数行和偶数列的pixels，图片变成原来的$\frac{1}{4}$大小

3 Benefit of Convolutional Layer

Fully Connected Layer不需要看整个图片，只需要重要的pattern👉receptive field某一些neurons一定要一摸一样👉parameter sharing
receptive field+parameter sharing=convolutional layer，虽然会有较大的model bias，但是convolutional layer是专门为影像设计的，所以用在image上偏差不会很大
用convolutional layer的network叫做CNN

4 Multiple Convolutional Layers

n个filters可形成feature map with n channels
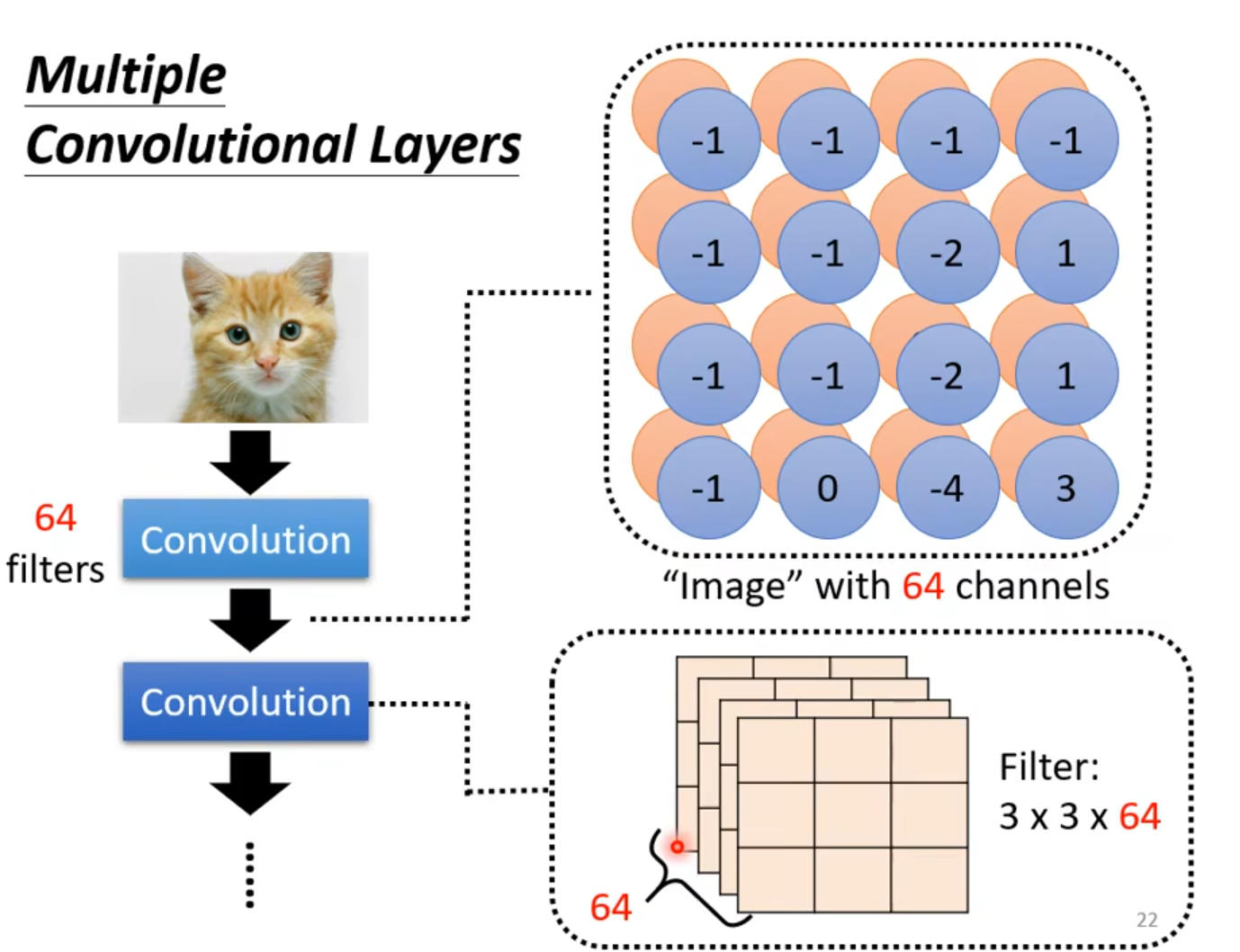
1. 先是将RGB图片放入convolution里，假设有64个filter(每个filter都是3x3x3)，那么就会得到一个 feature map(可以看作是一个新的图片，只是他的channels有64个)
2. 再把feature map放入convolution里，filter的大小为：3x3x64(filter的高度就是它要处理的image的channel)
filter比较小的情况下也能让network看比较大范围的pattern

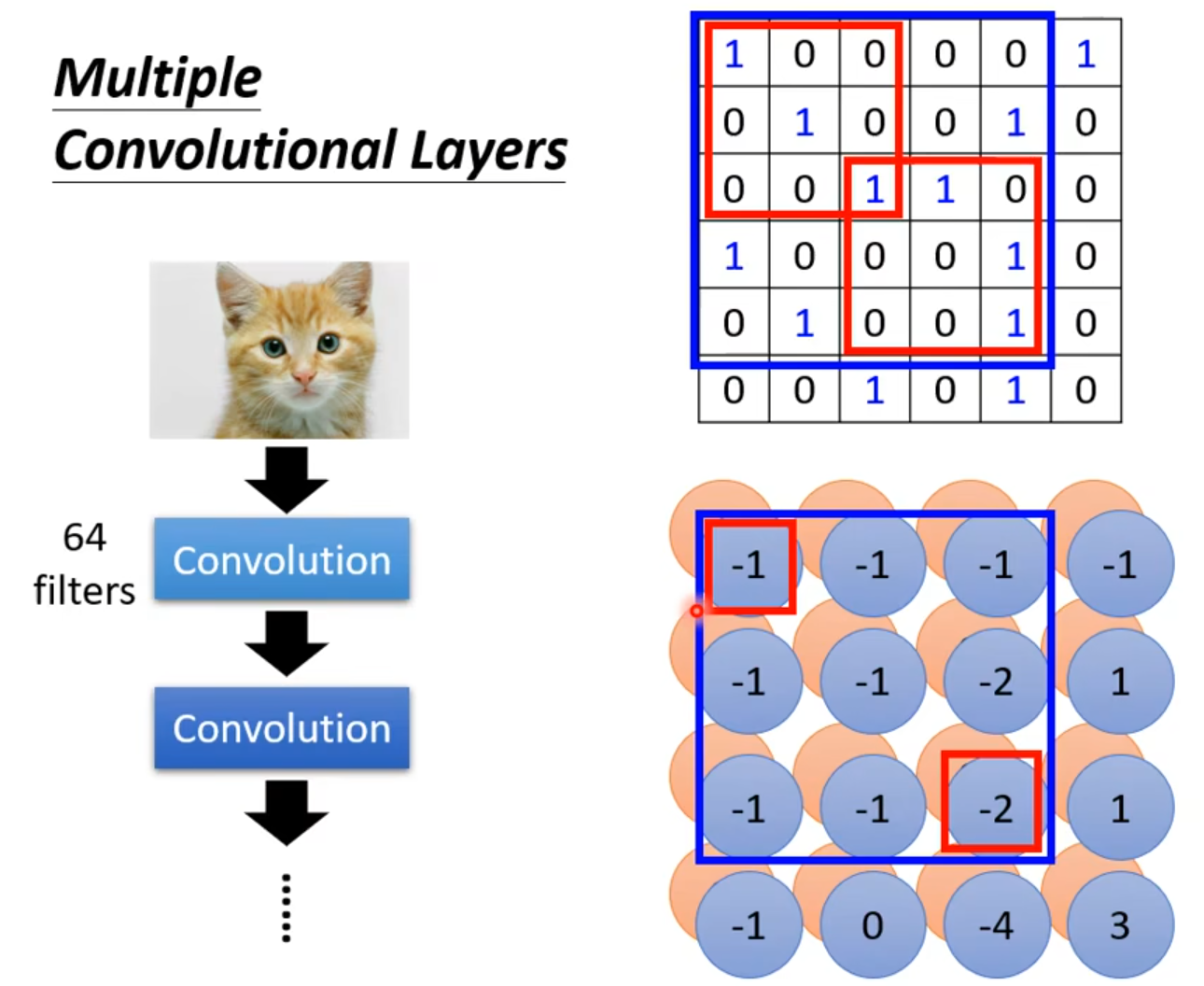
右下角蓝色圆圈的是其中一个filter，右上角是image，image左上角红色框对应filter左上角红色框，image右下角红色框对应filter右下角红色框。feature map的3x3对应image的5x5
5 Pooling - Max Pooling
在feature map中，n x n个数字一组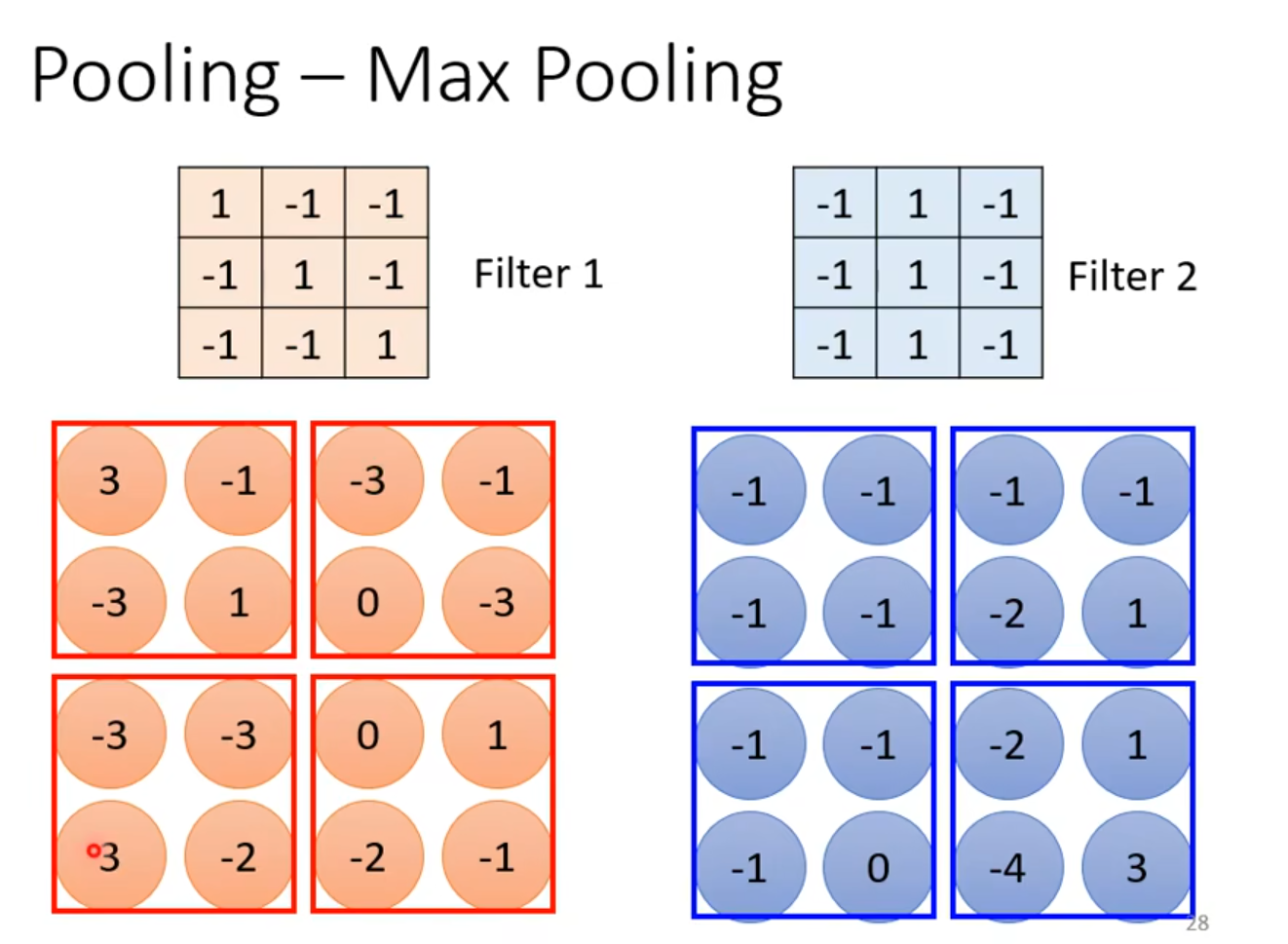
👉
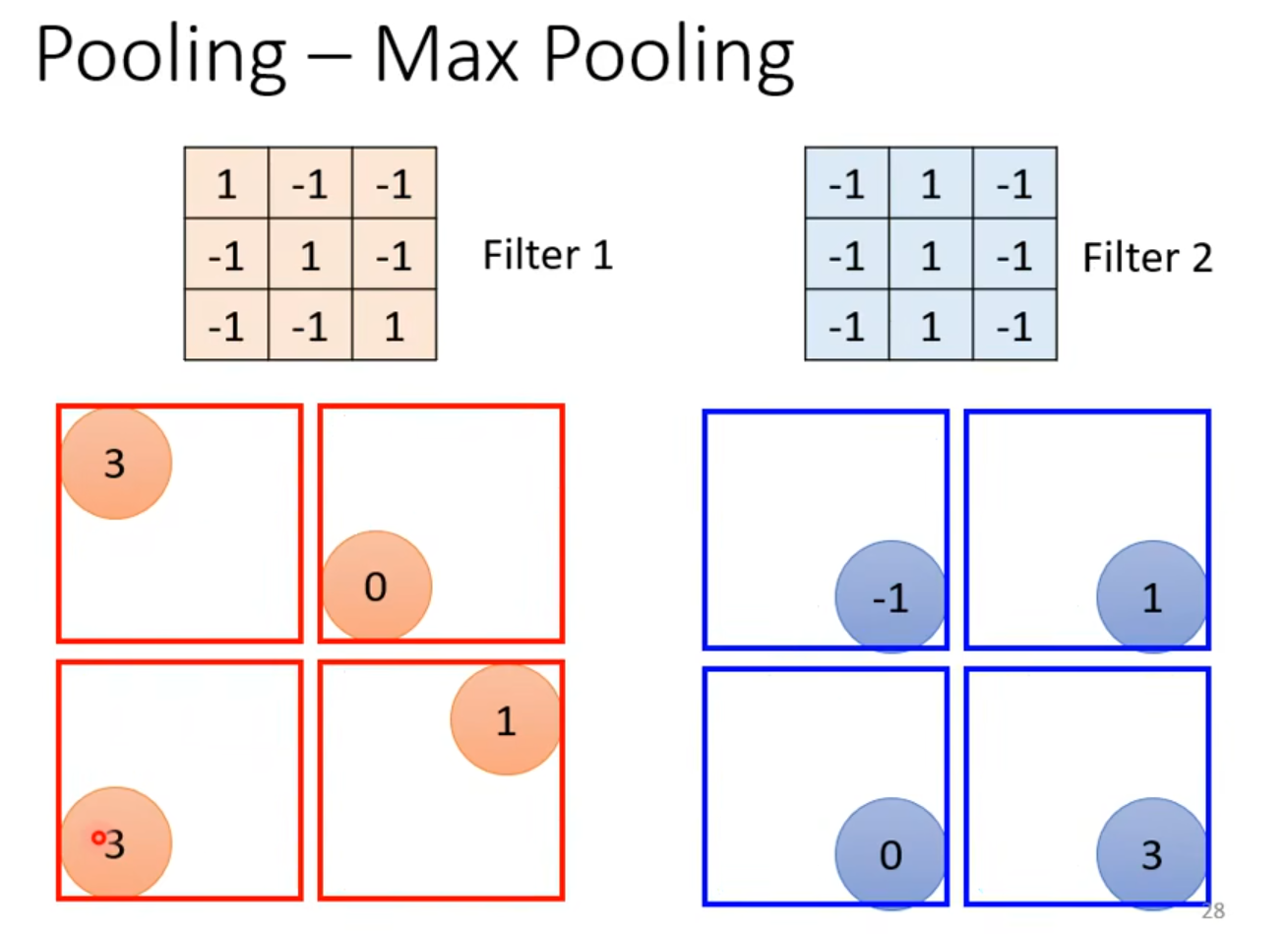
max pooling就是选一组里最大的那个数
做完convolution之后通常会搭配pooling，pooling不改变channels，但是改变长宽

6 The whole CNN

Flatten：将pooling的output本来矩阵的样子拉直

7 Application: Playing Go

Alpha Go uses 5x5 for first layer，可能是5x5的范围比较重要
同样可能存在相同的patters在不同的regions里
不用pooling

8 实操

8.1 Code

import torchvision.transforms as transforms

image_data = ...  # Your image data here

# Applying the transformations
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.1307,), (0.3081,))
])

transformed_data = transform(image_data)

8.2 原理

9 Advanced CNN

当训练次数过多时会发生过拟合，因此并不是训练次数越多模型准确度越高
解决梯度消失(过拟合)，使用Residual net

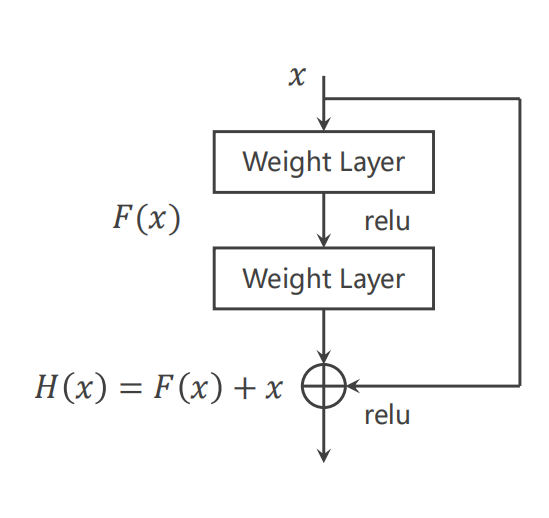
$z=H(x)$
$\dfrac{\partial z}{x}=\dfrac{\partial F(x)}{\partial x} + \dfrac{\partial x}{\partial x}=\dfrac{\partial F(x)}{\partial x}+1$
梯度=$\dfrac{\partial L}{\partial z}\times\dfrac{\partial z}{\partial x}$
当$\dfrac{\partial F}{\partial x}$很小的时候，$\dfrac{\partial z}{\partial x}$不会在0的附近