1.整体把握
LDA是一种主题模型,可以将文档集中每篇文档的主题以概率分布的形式给出,根据给定的一篇文章,反推其主题分布
一篇文档可以包含多个主题,文档中每一个词都由其中的一个主题生成
1.1LDA的图模型结构
类似贝叶斯网络结构

1.1.1贝叶斯的定义
节点表示随机变量${X_1,X_2,…,X_n}$,认为有因果关系(或非条件独立)的变量或命题用箭头来连接。如果用一个单箭头来连接,表示其中一个节点是“因(parents)”,另一个是“果(children)”,两节点就会产生一个条件概率值

👆圈表示随机变量(random variables),用箭头表示条件依赖(conditional dependencies)
令$G = (I,E)$表示一个有向无环图(DAG),其中I代表图形中所有的节点的集合,而E代表有向连接线段的集合,且令$X = (X_i),i ∈ I$为其有向无环图中的某一节点i所代表的随机变量,若节点X的联合概率可以表示成$p(x)=\prod\limits_{i\in I}p(x_i|x_{pa(i)})$,则称$X$为相对于一有向无环图G 的贝叶斯网络,其中,$pa(i)$表示节点i之“因”,或称$pa(i)$是$i$的parents(父母)。
联合概率:事件A和事件B同时发生的概率,记为$P(AB)$或$P(A,B)$或$P(A∩B)$
对于任意的随机变量,其联合概率可由各自的局部条件概率分布相乘得出:
$p(x_1,….,x_K)=p(x_K|x_1,….,x_{K-1})…p(x_2|x_1)p(x_1)$
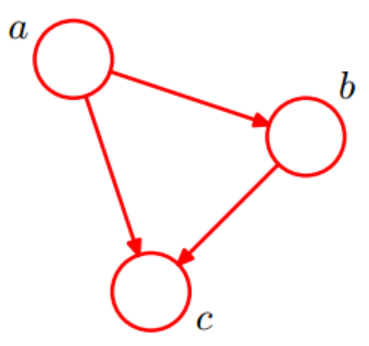
👆一个简单的贝叶斯网络(a导致b,a和b导致c)
$p(a,b,c)=p(c|a.b)p(b|a)p(a)$
1.2二项式分布
随机变量只有两个(非正即负),即重复n次的伯努利实验,记为$X\sim b(n,p)$
二项分布的概率密度函数为:
$P(K=k)=(n,k)p^k(1-p)^{n-k}$
对于k = 0, 1, 2, …, n,其中的
.jpg)
是二项式系数(这就是二项分布的名称的由来),又记为$\dfrac{n!}{k!(n-k)!}$
1.3多项式分布
由二项分布扩展到多维的情况
随机变量取值不是0-1,而是有多种离散值的可能(1,2,3,…,k)
假设有$i$个离散值,那么有$\sum_{i=1}^kp_i=1,p_i>0$
多项式分布的概率密度函数为:$P(x_1,x_2,…,x_k;n,p_1,p_2,…,p_k)=\dfrac{n!}{x_1!…x_k!}p^{x_1}…p^{x_k}$
1.4Gamma分布
Gamma函数实际意义:阶乘一般化,将阶乘推广到实数域
This content is only supported in a Feishu Docs
2.Beta分布
This content is only supported in a Feishu Docs
2.1Beta分布
beta是指一组定义在$(0,1)$区间的连续概率分布,有两个参数$\alpha$和$\beta$,且$\alpha,\beta>0$
二项分布的共轭先验分布
给定参数$\alpha>0$和$\beta>0$,取值范围为[0,1]的随机变量 x 的概率密度函数:$f(x;\alpha,\beta)=\dfrac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}$
其中$\dfrac{1}{B(\alpha,\beta)}=\dfrac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)},\Gamma(z)=\int_0^\infty t^{z-1}e^{-t}dt$
见pdf
2.2Beta-Binomial共轭
- 问题引入:
- 问题1:随机变量$X_1,X_2,…,X_n\sim^{idd}Uniform(0,1)$,把这n个随机变量排序后得到顺序统计量$X_{(1)},X_{(2)},…,X_{(n)}$,问$X_{(k)}$的分布是什么
- 问题2:$X_{(k)}$的分布是什么 <==> 猜测$p=X_{(k)}$,
- $Y_1,Y_2,…,Y_n\sim^{idd}Uniform(0,1)$,$Y_i$中有$m_1$个比$p$小,$m_2$个比$p$大,问$P(p|Y_1,Y_2,…Y_m)$的分布是什么
- 分析:
- 换言之,$Y_i$中有$m_1$个比$X_{(k)}$小,有$m_2$个比$X_{(k)}$大,所以$X_{(k)}$是$X_1,X_2,…,X_n,Y_1,Y_2,…,Y_n\sim^{idd}Uniform(0,1)$中第$k+m_1$大的数
- 事件服从Beta分布
- 可知$p=X_{(k)}$的密度概率函数为:$Beta(p|k+m_1,n-k+1+m_2)$
与贝叶斯结合过程
- 贝叶斯派思考问题的固定模式:
先验分布$\pi(\theta)$+ 样本信息$X$$\rightarrow$后验分布$\pi(\theta|x)$
在得到新的样本信息之前,人们对$\theta$的认知是先验分布$\pi(\theta)$,在得到新的样本信息
$X$后,人们对$\theta$的认知为$\pi(\theta|x)$
过程
- 为了猜测$p=X_{(k)}$,在获得一定的观测数据前,我们对$p$的认知是:$f(p)=Beta(p|k,n-k+1)$,此称为$p$的先验分布
- 为了获得结果$Y_i$中有$m_1$个比$p$小,$m_2$个比$p$大,针对$Y_i$做了$m$次伯努利实验,所以$m_1$服从二项分布$B(m,p)$
- 在得到$(m_1,m_2)$的数据后,$p$的后验分布为$f(p|m_1,m_2)=Beta(p|k+m_1,n-k+1+m_2)$
- 结合贝叶斯
- $Beta(p|k,n-k+1)+Count(m_1,m_2)=Beta(p|k+m_1,n-k+1+m_2)$
- 更一般的,对于非负实数$\alpha$和$\beta$:有如下关系$Beta(p|\alpha,\beta)+Count(m_1,m_2)=Beta(p|\alpha+m_1,\beta+m_2)$,其中$Count(m_1,m_2)$对应$B(m,p)$
- 针对这种观测到的数据符合以下条件的,就是Beta-Binomial共轭,换言之,Beta分布是二项式分布的共轭先验概率分布
- 条件一:二项分布
- 条件二:参数的先验分布和后验分布都是Beta分布
- 共轭先验分布→2.3
- 二项分布和Beta分布是共轭分布意味着,如果我们为二项分布的参数p选取的先验分布是Beta分布,那么以p为参数的二项分布用贝叶斯估计得到的后验分布仍然服从Beta分布
- $\alpha$和$\beta$可以认为是形状参数
2.3共轭先验分布
如果后验概率和先验概率满足同样的分布律,那么先验分布和后验分布被叫做共轭分布,同时,先验分布叫做似然函数的共轭先验分布。
比如,某观测数据服从概率分布P(θ)(先验)时,当观测到新的X数据(样本信息)时,我们一般会遇到如下问题:
- 可否根据新观测数据X,更新参数θ?
- 根据新观测数据可以在多大程度上改变参数θ,即$\theta \leftarrow \theta + \triangle \theta$
- 当重新估计θ的时候,给出新参数值θ的新概率分布,即P(θ|x)。
2.4从Beta分布推广到Dirichlet分布
见pdf
结论是:对于Beta分布的随机变量,其均值(期望)可以用$\dfrac{\alpha}{\alpha+\beta}$来估计
类比到Dirichlet分布:如果$\mathop{p}\limits^{\rightarrow}\sim Dir(\mathop{t}\limits^{\rightarrow}|\mathop{\alpha}\limits^{\rightarrow})$,那么有$E(\mathop{p}\limits^{\rightarrow})=(\dfrac{\alpha_1}{\sum^K_{i=1}\alpha_i},\dfrac{\alpha_2}{\sum^K_{i=1}\alpha_i},…,\dfrac{\alpha_3}{\sum^K_{i=1}\alpha_i})$
3.Dirichlet分布
是beta分布在高纬度上的推广
$f(x_1,x_2,…,x_k;\alpha_1,\alpha_1,…,\alpha_k)=\dfrac{1}{B(\alpha)}\prod_{i=1}^kx_{i}^{a^i-1}$
其中$B(\alpha)=\dfrac{\prod_{i=1}^k\Gamma(a^i)}{\Gamma(\sum_{i=1}^k)a^i},\sum x_i=1$
3.1Dirichlet分布
This content is only supported in a Feishu Docs
3.2Dirichlet-Multinomial共轭
- 问题引入:在2.2的问题2的基础上继续深入
- 问题3:随机变量$X_1,X_2,…,X_n\sim^{idd}Uniform(0,1)$,把这n个随机变量排序后得到顺序统计量$X_{(1)},X_{(2)},…,X_{(n)}$,问$(X_{(k_1)},X_{k_1+k_2})$的联合分布是什么
- 计算见pdf
- 为论证Dirichlet分布是多项式分布的共轭先验概率分布,在问题3的基础上继续深入
- 问题4:
- 随机变量$X_1,X_2,…,X_n\sim^{idd}Uniform(0,1)$,把这n个随机变量排序后得到顺序统计量$X_{(1)},X_{(2)},…,X_{(n)}$
- 令$p_1=X_{k_1},p_2=X(k_1+k_2),p_3=1-p_1-p_2$,现在要猜测$\mathop{p}\limits^{\rightarrow}=(p_1,p_2,p_3)$
- $Y_1,Y_2,…,Y_m\sim^{idd}Uniform(0,1)$,$Y_i$中落到$(0,p_1],[p_1,p_2),[p_2,1]$三个区间的个数分别为$m_1,m_2,m_3$,$m=m_1+m_2+m_3$
- 问后验分布$P(\mathop{p}\limits^{\rightarrow}|Y_1,Y_2,…Y_m)$的分布是什么
- 讨论见pdf
- 问题4:
- 问题3:随机变量$X_1,X_2,…,X_n\sim^{idd}Uniform(0,1)$,把这n个随机变量排序后得到顺序统计量$X_{(1)},X_{(2)},…,X_{(n)}$,问$(X_{(k_1)},X_{k_1+k_2})$的联合分布是什么
- 与贝叶斯结合推理:
- 要猜测参数$\mathop{p}\limits^{\rightarrow}=(p_1,p_2,p_3)$,其先验分布为$Dir(\mathop{p}\limits^{\rightarrow}|\mathop{k}\limits^{\rightarrow})$
- $Y_1,Y_2,…,Y_m\sim^{idd}Uniform(0,1)$,$Y_i$中落到$(0,p_1],[p_1,p_2),[p_2,1]$三个区间的个数分别为$m_1,m_2,m_3$,所以$\mathop{m}\limits^{\rightarrow}=(m_1,m_2,m_3)$服从多项分布$Mult(\mathop{m}\limits^{\rightarrow}|\mathop{p}\limits^{\rightarrow})$
- 给定了来自数据提供的$\mathop{m}\limits^{\rightarrow}$后,$\mathop{p}\limits^{\rightarrow}$的后验分布变为$Dir(\mathop{p}\limits^{\rightarrow}|\mathop{k}\limits^{\rightarrow}+\mathop{m}\limits^{\rightarrow})$
- 直观表述:
- $Dir(\mathop{p}\limits^{\rightarrow}|\mathop{k}\limits^{\rightarrow})+MultCount(\mathop{m}\limits^{\rightarrow})=Dir(\mathop{p}\limits^{\rightarrow}|\mathop{k}\limits^{\rightarrow}+\mathop{m}\limits^{\rightarrow})$
- 令$\mathop{\alpha}\limits^{\rightarrow}=\mathop{k}\limits^{\rightarrow},可以把$\mathop{\alpha}\limits^{\rightarrow}$从整数集合延拓到实数集合,从而得到更一般的表达:
- $Dir(\mathop{p}\limits^{\rightarrow}|\mathop{\alpha}\limits^{\rightarrow})+MultCount(\mathop{m}\limits^{\rightarrow})=Dir(\mathop{p}\limits^{\rightarrow}|\mathop{\alpha}\limits^{\rightarrow}+\mathop{m}\limits^{\rightarrow})$
- 结论:
- 观测到的数据符合多项分布
- 参数的先验分布和后验分布都是Dirichlet分布
- 就是Dirichlet-Multinomial共轭
- 一般形式的Dirichlet分布定义和对于给定的$\mathop{p}\limits^{\rightarrow}$和$N$,其多项式分布见pdf
- Dirichlet分布$Dir(\mathop{p}\limits^{\rightarrow}|\mathop{\alpha}\limits^{\rightarrow})$和多项分布$MultCount(\mathop{n}\limits^{\rightarrow}|\mathop{p}\limits^{\rightarrow},N)$是共轭关系
4.LDA模型
定义的变量
- $w$表示词,$V$表示所有单词的个数(固定值)
- $z$表示主题,是主题的个数(预先给定,固定值)
- $D(w_1,…,w_M)$表示语料库,其中的$M$是语料库中的文档数(固定值)
- $\mathbf{w}=(w_1,w_2,…,w_N)$表示文档,其中的$N$表示一个文档中的词数(随机变量)
4.1各个模型基础
4.1.1Unigram model
对于文档$\mathbf{w}=(w_1,w_2,…,w_N)$,用$p(w_n)$表示词$w_n$的先验概率,生成文档$\mathbf{w}$的概率为:$p(\mathbf{w})=\sum^N_{n=1}p(w_n)$
图模型为
- 图模型一
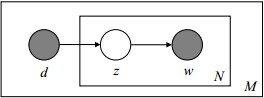
- (图中被涂色的w(word)表示可观测变量,N表示一篇文档中总共N个单词,M表示M篇文档)
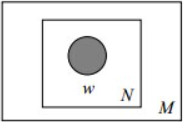
- 图模型二

- nigram model假设文本中的词服从Multinomial分布,而我们已经知道Multinomial分布的先验分布为Dirichlet分布。上图中的$w_n$表示在文本中观察到的第n个词,$n\in[1,N]$表示该文本中一共有$N$个单词。加上方框表示重复,即一共有$N$个这样的随机变量$w_n$。其中,$p$和$\alpha$是隐含未知变量:
- $p$是词服从的Multinomial分布的参数
- $\alpha$是Dirichlet分布(即Multinomial分布的先验分布)的参数
- 一般$\alpha$由经验事先给定(先验),$p$由观察到的文本中出现的词学习得到(样本),表示文本中出现每个词的概率
4.1.2Mixture of unigrams model
该模型的生成过程是:给某个文档先选择一个主题$z$,再根据该主题生成文档,该文档中的所有词都来自一个主题。假设主题有$z_1,…z_k$,生成文档$\mathbf{w}$的概率为:
$p(\mathbf{w})=p(z_1)\prod^N_{n=1}p(w_n|z_1)+…+p(z_k)\prod^N_{n=1}p(w_n|z_k)=\sum_zp(z)\prod^N_{n=1}p(w_n|z)$
图模型为:(图中被涂色的w表示可观测变量,未被涂色的z表示未知的隐变量,N表示一篇文档中总共N个单词,M表示M篇文档)
.jpg)
4.2PLSA模型
建议直接看这个
4.2.1pLSA模型下生成文档

4.2.2根据文档反推其主题分布


4.2.3EM算法
This content is only supported in a Feishu Docs
4.2.3.1EM算法的简单介绍
隐变量$Z=(z_1,z_2,z_3,z_4,z_5)$代表每一轮所使用的硬币
所以第一步先估算$Z$,这步同时是E-step
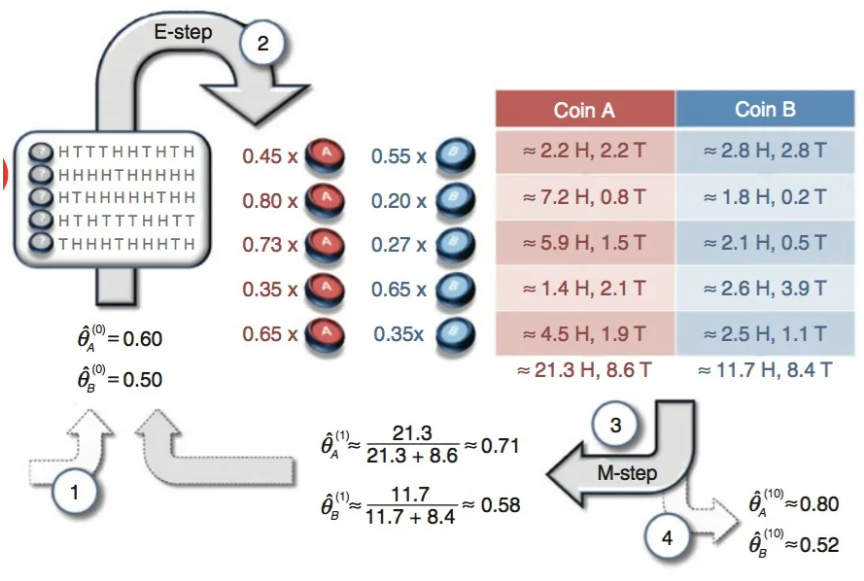
👆流程:
- 随机初始化$\theta_A=0.6$和$\theta_B=0.5$(E-step)
- H代表正面,T代表反面;对于第一轮来说,实际的情况是5个正的5个反的,进行如下计算
- $P_A=\dfrac{0.6^50.4^5}{(0.6^50.4^5)+(0.5^5+0.5^5)}=0.45$
- $P_B=\dfrac{(0.5^5+0.5^5)}{(0.6^5*0.4^5)+(0.5^5+0.5^5)}=0.55$
- 对于第一轮抛掷,该枚硬币是硬币A的概率为0.45,是硬币B的概率为0.55,其他轮同理,这一步得到了Z的概率分布
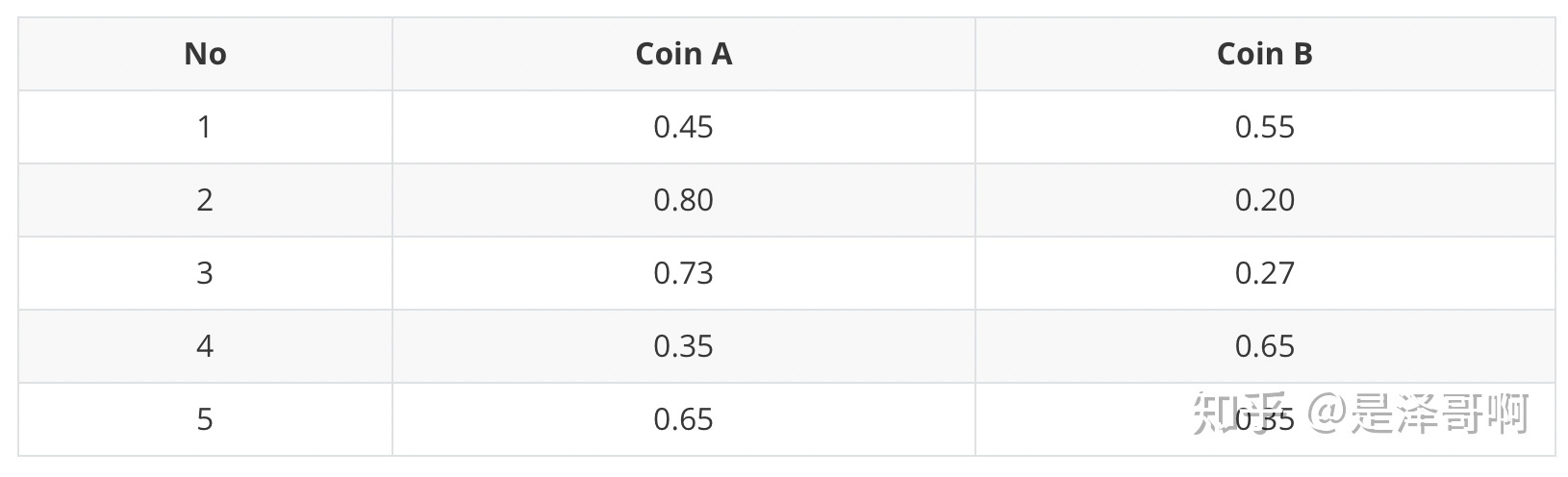
- 利用期望求硬币A和硬币B的贡献,对于第一轮来说
- H:0.45*5=2.25
- T:0.55*5=2.75
- 其他轮同理
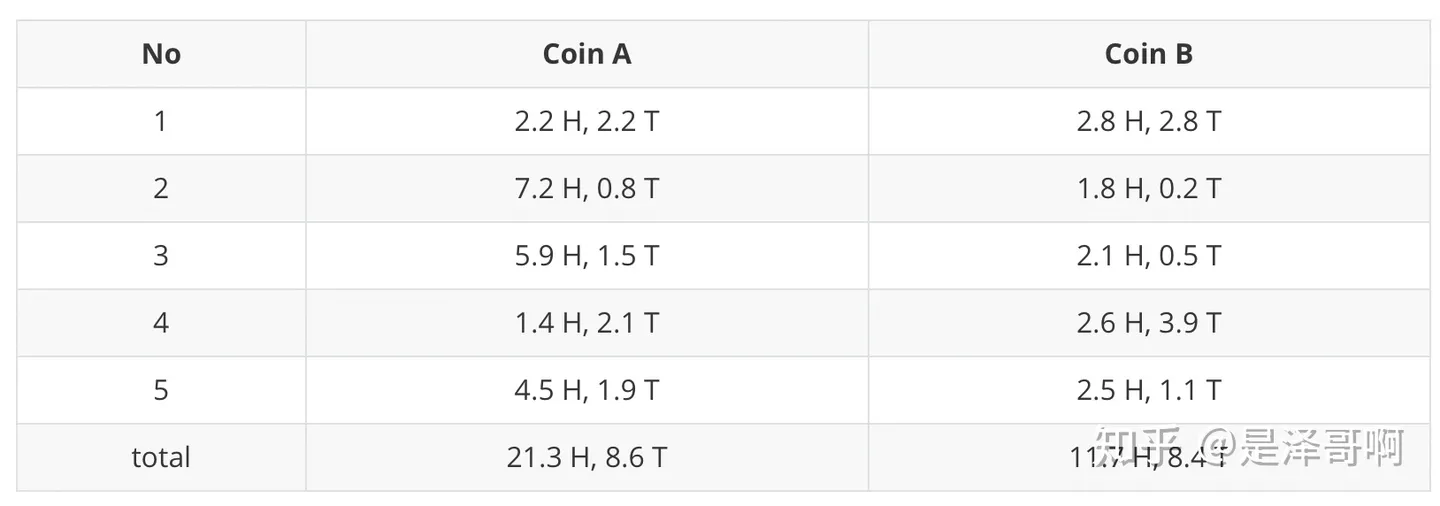
- 用极大似然估计来估计新的$\theta_A$和$\theta_B$,这步就是M-Step
- $\theta_A=\dfrac{21.3}{21.3+8.6}=0.71$
- $\theta_B=\dfrac{11.7}{11.7+8.4}=0.58$
- 如此反复迭代,可以算出最终的参数值
- $L(\theta)$与$J(z,Q)$的关系
- 这张图的意思是
- 先固定$\theta$,调整$Q(z)$使下界$J(z,Q)$上升至与$L(\theta)$在该$\theta$值下相同(由绿线到蓝线)
- 然后固定$Q(z)$,调整$\theta$使下界$J(z,Q)$达到最大值
- 再固定$\theta$…
- 直到收敛到似然函数$L(\theta)$的最大值时,得到该处的$\theta^{*}$
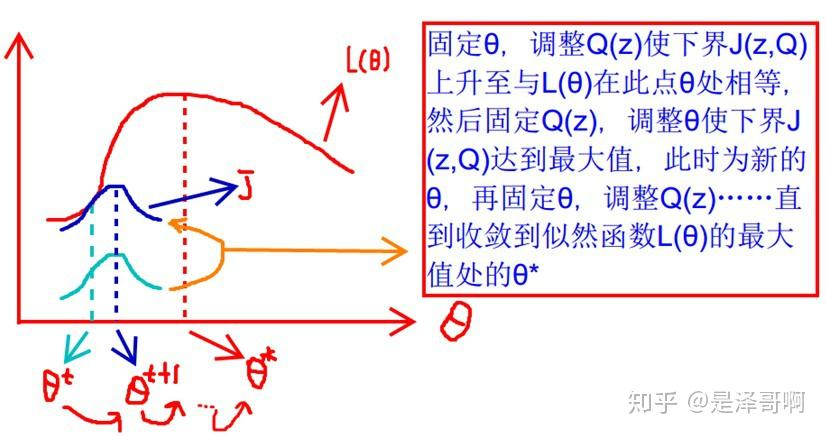
- EM算法的整体框架
Repeat until convergence{
(E-step) For each
$i$
,set
$Q_i(z):=p(z^{(i)}|x^{(i)};\theta)$ 找隐变量的分布(直线往上移)
(M-step) Set
$\theta:=arg max_{\theta}\sum_i\sum_{z^{(i)}}log\dfrac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$ 找新的$\theta$(点位往左右移)
}
4.2.3.2EM算法估计pLSA的两个未知参数
从矩阵角度描述带估计的两个未知变量$P(w_j|z_k)$和$P(z_k|d_i)$
词表$V$有$j$个词项;所有主题$Z$有$k$个主题;有$i$篇文章
- 假定用$\phi_k$表示词表$V$在主题$z_k$上的一个多项分布,则$\phi_k$可以表示成一个向量,每个元素$\phi_{k,j}$表示词项$w_j$出现在主题$z_k$中的概率,即:
- $P(w_j|z_k)=\phi_{k,j}$,$\sum_{w_j\in V}\phi_{k,j}=1$
- 假定用$\theta_i$表示所有主题$K$在文档$d_i$上的一个多项分布,则$\theta_i$可以表示成一个向量,每个元素$\theta_{i,k}$表示主题$z_k$出现在文档$d_i$中的概率,即:
- $P(z_k|d_i)=\theta_{i,k}$,$\sum_{z_k\in K}\theta_{i,k}=1$
$P(w_j|z_k)$和$P(z_k|d_i)$转换成了两个矩阵,换言之,我们要求解的参数就是这两个矩阵:
- $\Phi=[\phi_1,…\phi_K], z_k\in Z$
- $\Theta=[\theta_i,…,\theta_M],d_i\in D$
词和词之间是相互独立的,整篇文档$N$个词的分布为:
- $P(W|d_i)=\prod_{j=1}^NP(d_i,w_j)^{n(d_i,w_j)}$
文档和文档之间也是相互独立的,整个语料库($M$篇文档,每篇文档$N$个词)中词的分布为
- $P(W|D)=\prod_{i=1}^M\prod_{j=1}^NP(d_i,w_j)^{n(d_i,w_j)}$
其中,
$n(d_i,w_j)$表示词项$w_j$在文档$d_i$中的词频
$n(d_i)$表示文档$d_i$中文档词的总数
显然有$n(d_i)=\sum_{w_j\in V}n(d_i,w_j)$,一篇文档中词的总数等于词表中每个词出现的次数之和
整个语料库的词分布的对数似然函数:
$\begin{align} l(\Phi,\Theta)&=\sum_{i=1}^{M}\sum_{j=1}^Nn(d_i,w_j)logP(d_i,w_j)\\ &=\sum_{i=1}^Mn(d_i)\left(logP(d_i)+\sum_{j=1}^N\dfrac{n(d_i,w_j)}{n(d_i)}log\sum_{k=1}^KP(w_j|z_k)P(z_k|d_i)\right)\\ &=\sum_{i=1}^Mn(d_i)\left(logP(d_i)+\sum_{j=1}^N\dfrac{n(d_i,w_j)}{n(d_i)}log\sum_{k=1}^K\phi_{k,j}\theta_{i,k}\right) \end{align}$
- (1)对应的是$L(\theta)\geq\sum_{i=1}^n\sum_z^ZQ_i(z)log\dfrac{P(x_i,z;\theta)}{Q_i(z)}$,其中$Q_i(z)$表示的是样本$i$隐含变量$z$的某种分布;$log\dfrac{P(x_i,z;\theta)}{Q_i(z)}$表示的是对数似然函数
- (2)分别求文本的对数似然函数和词的对数似然函数,见pdf
- (3)就是上面得到的以矩阵的形式表达多项式分布
多元函数在有约束条件$\sum_{j=1}^{M}\theta_{k,j}=1$和$\sum_{k=1}^K\phi_{i,k}=1$下求极值,用拉格朗日乘数法(即通过引入拉格朗日乘子将约束条件和多元(目标)函数融合到一起,转化为无约束条件的极值问题)见pdf
总结:
- 为求得$P(w_j|z_k)$和$P(z_k|d_i)$,因此用EM算法去估计$\theta=(P(w_j|z_k),z_k|d_i)$这个参数
- $\phi_{k,j}$表示词项$w_j$出现在主题$z_k$中的频率,即$P(w_j|z_k)=\phi_{k,j}$,从而把$P(w_j|z_k)$转换成矩阵$\Phi$
- $\theta_{i,k}$表示主题$z_k$出现在文档$d_i$中的频率,即$P(z_k|d_i)=\theta_{k,i}$,从而把$P(z_k|d_i)$转换成矩阵$\Theta$
- 最后通过EM算法求出两个矩阵
4.2.3.2.1拉格朗日乘数法
- 没有约束条件
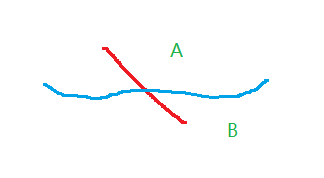
目标函数$f(x,y)$是一座山的高度,约束$g(x,y)$是镶嵌在山上的一条曲线,如下图
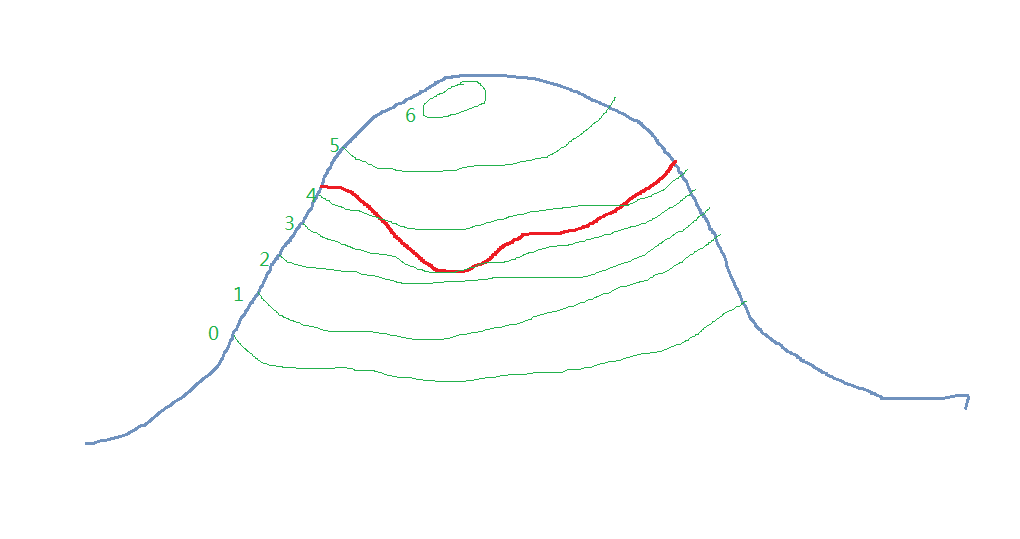
红线是约束曲线
目的:找红线上的最低点
步骤:
- 从第0条线开始往上数,数到第三条,与约束曲线有交点,比第三条低的地方都不在约束范围内,所以这是约束曲线的最低点
- 约束曲线不会和等高线相交,一定是相切,如果是相交的话,约束曲线有一部分在最低点的曲线的下端(即目标曲线并不能包括约束曲线的最低点),如下图中约束曲线有一部分在B区域,但是B区域比等高线低
- 那么两条线只能相切,意味他们的法线平行<==>法向量只差一个任意的常数乘子(取-$\lambda$):
- ∇$f(x,y)=-\lambda$∇$g(x,y)$
- ∇$f(x,y)+\lambda$∇$g(x,y)=0$
见pdf
4.3LDA模型
4.3.1pLSA和LDA的对比:生成文档与参数估计
👇频率派vs贝叶斯派
This content is only supported in a Feishu Docs
LDA模型中一篇文档生成的方式:
- 按照先验分布$P(d_i)$选择一篇文档$d_i$
- 从Dirichlet分布$\alpha$中取样生成文档$d_i$的主题分布$\theta_i$,即主题分布$\theta_i$由超参数为$\alpha$的Dirichlet分布生成①
- 从主题的多项式分布$\theta_i$中取样生成文档$d_i$第$j$个词的主题$z_{i,j}$
- 从Dirichlet分布$\beta$中取样生成主题$z_{i,j}$对应的词语分布$\phi_{z_i,j}$,即词语分布$\phi_{z_i,j}$由参数为$\beta$的Dirichlet分布生成②
- 从词语的多项式分$\phi_{z_i,j}$中采样最终生成词语$w_{i,j}$
👇LDA和pLSA的区别:
- LDA是pLSA的贝叶斯版本,主题分布和词分布本身都由先验知识随机给定
- ①②LDA在pLSA的基础上为主题分布和词分布加了两个Dirichlet先验分布$\alpha$和$\beta$
- pLSA中主题分布和词分布是唯一确定的,但是LDA中主题分布和词分布不再唯一确定不变,即无法确切给出,但是再怎么变化也依然服从一定的分布,即主题分布和词分布由Dirichlet先验随机确定
- 文本生成后,两者都要根据文档去推断主题分布和词分布,只是用的参数推断方法不同
- pLSA中用极大似然估计的思想
- LDA中把两个参数视为随机变量,加入Dirichlet先验
- pLSA属于频率派思想,样本随机,参数($\theta_{k,j}$和$\phi_{i,j}$)虽未知但固定;LDA属于贝叶斯派思想,样本固定,参数($\theta_i$和$\phi_{z_i,j}$)未知但不固定,是个随机变量,服从一定的分布(Dirichlet分布)
- pLSA中
- 主题分布和词分布确定后,以一定概率$\left(P(z_k|d_i),P(w_j|z_k)\right)$分别选取具体的主题和词项,生成好文档
- 然后根据生成好的文档反推其主题分布、词分布
- 最终用EM算法求解出两个未知但固定的参数的值:
- $\phi_{k,j}$(由$P(w_j|z_k)$转换而来)
- $\theta_{i,k}$(由$P(z_k|d_i)$转换而来)
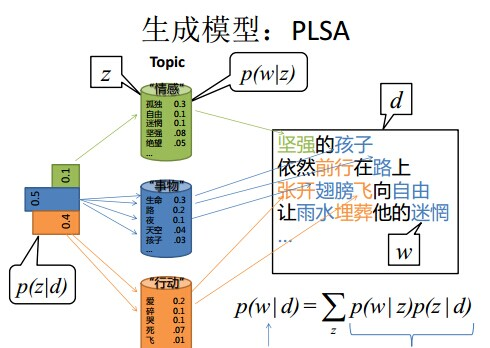
- LDA**中**
- 主题分布和词分布是随机变量(即文档$d_i$产生主题$z_k$和主题$z_k$产生词项$w_j$的概率都是随机变量)
- Dirichlet先验为文档$d_i$生成主题分布$\Theta$,然后根据主题分布$\Theta$产生主题$z_k$
- 从无穷多个主题分布中按照Dirichlet先验随机抽取出某个主题分布出来
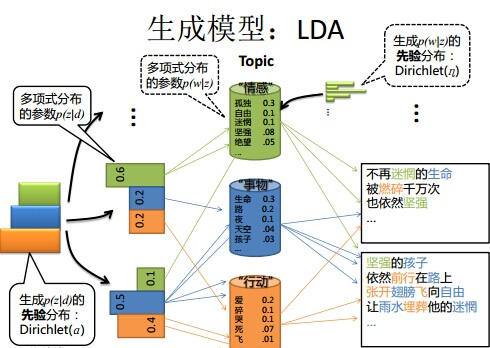
- pLSA中
- 例子
- 好比,去一朋友家:
- 按照频率派的思想,我估计他在家的概率是1/2,不在家的概率也是1/2,是个定值。
- 而按照贝叶斯派的思想,他在家不在家的概率不再认为是个定值1/2,而是随机变量。比如按照我们的经验(比如当天周末),猜测他在家的概率是0.6,但这个0.6不是说就是完全确定的,也有可能是0.7。如此,贝叶斯派没法确切给出参数的确定值(0.3,0.4,0.6,0.7,0.8,0.9都有可能),但至少明白在哪个范围或哪些取值(0.6,0.7,0.8,0.9)更有可能,哪个范围或哪些取值(0.3,0.4) 不太可能。进一步,贝叶斯估计中,参数的多个估计值服从一定的先验分布,而后根据实践获得的数据(例如周末不断跑他家),不断修正之前的参数估计,从先验分布慢慢过渡到后验分布。
- 好比,去一朋友家:
4.3.2LDA生成文档—三维坐标系
4.3.3pLSA和LDA概率图对比
z跟w都得是小写,阴影圆圈表示可观测的变量,非阴影圆圈表示隐变量或参数,箭头表示两变量间的条件依赖性,方框表示重复抽样,方框右下角的数字代表重复抽样的次数
- pLSA
- LDA
.jpg)
- 假定语料库中共有M篇文章,每篇文章下的Topic的主题分布是一个从参数为$\alpha$的Dirichlet先验分布中采样得到的Multinomial分布,每个Topic下的词分布是一个从参数$\beta$为的Dirichlet先验分布中采样得到的Multinomial分布。
- 对于某篇文章中的第n个词,首先从该文章中出现的每个主题的Multinomial分布中选择或采样一个主题,然后再在这个主题对应的词的Multinomial分布中选择或采样一个词。不断重复这个随机生成过程,直到M篇文章全部生成完成。
- M 篇文档会对应于 M 个独立的 Dirichlet-Multinomial 共轭结构,K 个 topic 会对应于 K 个独立的 Dirichlet-Multinomial 共轭结构
- $\alpha\rightarrow\theta\rightarrow z$表示生成文档中的所有词对应的主题
- $\alpha\rightarrow\theta$对应的是Dirichlet分布
- $\theta\rightarrow z$对应的是Multinomial分布
- 因此整体是一个Dirichlet-Multinomial共轭结构
- $\beta\rightarrow\theta\rightarrow w$表示某个主题对应的词
- 同上
- $\alpha\rightarrow\theta\rightarrow z$表示生成文档中的所有词对应的主题
4.3.4pLSA和LDA参数估计方法的对比
- pLSA
- 使用EM算法估计$\Phi$和$\Theta$,使用的思想是极大似然估计
- LDA
- 估计$\Phi$和$\Theta$可用变分(Variational inference)-EM算法,也可以用gibbs采样,前者的思想是最大后验估计MAP(MAP与MLE类似,都把未知参数当作固定的值),后者的思想是贝叶斯估计
4.3.5Gibbs采样
Gibbs抽样是马尔可夫链蒙特卡尔理论(MCMC)中用来获取一系列近似等于指定多维概率分布(比如2个或者多个随机变量的联合概率分布)观察样本的算法。
5.代码实现
This content is only supported in a Feishu Docs
5.1corpora.Dictionary(texts):
为每个出现在语料库中的单词分配了一个独一无二的编号id
5.2dictionary.doc2bow():
把文档变成一个稀疏向量,[(0,1), (1,1)],表明id为0,1的词汇出现了一次,而其他词汇没有出现
5.3models.Ldamodel:
参数:
corpus:一组文档的语料库,是list of list of tuple的形式,每个list内的元素是(word_id, count),表示一个文档中每个词出现的次数
num_topics:主题数量
id2word:将每个词的id映射到该词的字符串表示
passes:在拟合模型中要执行的迭代次数
random_state:随机数生成器的种子
5.4ldamodel.show_topics
用于展示LDA模型的主题函数
5.4.1x
格式:
[
(主题1,[(关键词1.1,概率1.1),(关键词1.2,概率1.2)…]),
(主题2,[(关键词2.1,概率2.1),(关键词2.2,概率2.2)…]),
(),
….]
.jpg)
5.4.2tp
tp[0]—>主题
tp[1]—>[(关键词1,概率1),(关键词2,概率2)…]
5.4.3打印每个主题下每个单词的概率
This content is only supported in a Feishu Docs
👇用.split()函数
- 先按照”+”号进行拆分
- 然后对于以”+”号拆分出来的东西,再以”*”号进行拆分
- 打印格式:”单词”(单词出现的概率)

5.4.4计算一致性
CoherenceModel(model, texts, dictionary, coherence)
model:指定用于计算一致性的主题模型对象(ldamodel)
text:指定一个文本列表
dictionary:指定一个词典对象
coherence:指定要计算的一致性指标
- C_V:衡量主题内部的一致性和主题之间的互异性
返回的是一致性评分,分数越高,表示主题模型的主题更具有一致性,一致性评分仅用于比较不同主题模型之间的一致性
This content is only supported in a Feishu Docs
发现,当主题数目为10的时候,十个不同的主题之间的coherence值较大,一致性较高。这四个主题下的关键词能够很好地概括所有文档的关键词
6.没懂的地方
- 第四行到第五行